A partir del análisis de las funciones, regla de la primera y segunda derivada, puntos críticos, inflexiones

Los dos números han de cumplir:

$$\begin{align}&x^2+y^2=100\end{align}$$

La función a optimizar es el producto de los números que queremos que sea máximo:

$$\begin{align}&P(x,y)=x·y\\&\\&y=\sqrt{100-x^2}\\&\\&P(x)=x \sqrt{100-x^2}=\sqrt{100x^2-x^4}\\&\\&Dominio \ P(x)=[-10,10]\\&\\&P'(x)=\frac{1}{2 \sqrt{100x^2-x^4}}(200x-4x^3)\\&\\&Extremos \ relativos:\\&\\&P'(x)=0 \Rightarrow 200x-4x^3=0  \Rightarrow  x(200-4x^2)=0\\&x_1=0\\&x_2=\sqrt {\frac{200}{4}}=\sqrt {50} \simeq 7.07\\&\\&x_3=- \sqrt{50}\end{align}$$

Como la segunda derivada es un poco liosa, aplicaré el criterio de la primera derivada para comprobar los máximos y mínimos relativos. Este criterio consiste en estudiar el crecimiento de la función en los diferentes intervalos:

$$\begin{align}&Intervalos \ de \ crecimiento:\\&\\&(-10,-\sqrt {50}) \Rightarrow f'(-8)>0 \Rightarrow creciente\\&\\&(-\sqrt {50}, 0)  \Rightarrow f'(-5)<0 \Rightarrow decreciente\\&\\&(0,+\sqrt{50})  \Rightarrow f'(2)>0 \Rightarrow creciente\\&\\&(+ \sqrt {50} ,10)  \Rightarrow f'(8)<0 \Rightarrow decreciente\end{align}$$

El máximo está en :

$$\begin{align}&x=\sqrt {50} \Rightarrow y=\sqrt {50}\\&\\&x=-\sqrt {50} \Rightarrow y=-\sqrt {50}\\&\\&producto \ máximo:\\&\\&P=\sqrt{50}·\sqrt{50}=50\end{align}$$

Te pongo la gráfica de la función P(x):

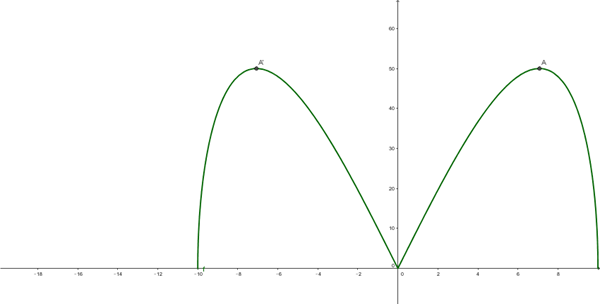
Saludos

;

;)