Es una función racional. Su dominio son todos los números Reales excepto los que anulan el denominador:
x-2=0 ===> x=2 ===>
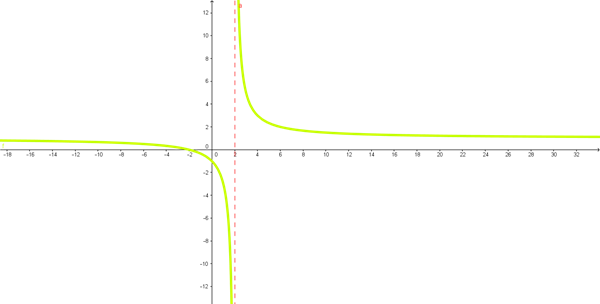
$$\begin{align}&Domf(x)= \mathbb R -\{2 \}\\&\\&\lim_{x \to 2} \frac{x+2}{x-2}=\frac{4}{0}=\infty\\&Asíntotata \ vertical \ \ x=2\\&\\&\\&Asíntota \ horizontal :\\&\\&\lim_{x \to \pm \infty} \frac{x+2}{x-2}=\lim_{x \to 2} \frac{x}{x}=1\\&\\&Asíntota \ horizontal \ \ y=1\\&Corte \ con \ el \ eje \ OX: \ y=0=\frac{x+2}{x-2} \Rightarrow x+2=0 \Rightarrow x=-2\\&\\&Corte \ con \ el \ eje \ OY: x=0 \Rightarrow f(0)=\frac{0+2}{0-2}=-1\\&\\&Crecimiento:Max \ y \ mínimos:\\&\\&y'=\frac{1(x-2)-(x+2)1}{(x-2)^2}=\frac{-4}{(x-2)^2}\\&\\&y'=0 \Longrightarrow\\&\\&\frac{-4}{(x-2)^2}=0 \Rightarrow -4=0 \ \ \ \not \exists solución \Rightarrow no \ hay \ max \ ni \ min\\&\\&y'<0 \ \ \ \forall x\\&\\&\\&\end{align}$$la derivada es negativa para todo x, ya que el numerador es negativo y el denominador positivo (está al cuadrado).Luego la función es siempre decreciente:
SAludos
;
;)

