El perímetro de un triangulo, determinar medida de ac y bc
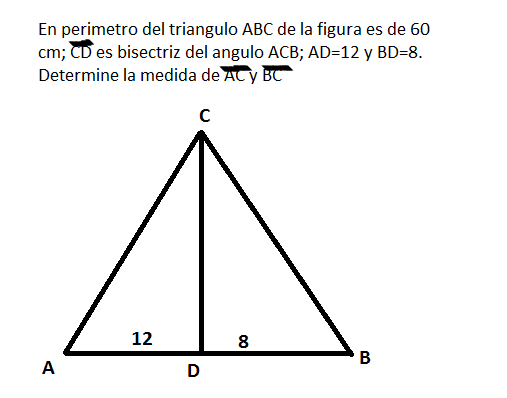
Calcular el perimetro del triangulo AbC de la figura es de 60 cm; CD es bisectriz del angulo ACB; AD=12 y BD=8. DETERMINAR LA MEDIDA DE AC Y BC.
Si pudieran ayudarme
Si el perímetro es 60, entonces tenemos:
AC + BC + AB = 60
Reemplazando:
AC + BC + 20 = 60
AC + BC = 40 ...................... (I)
Luego, por el teorema de la bisectriz interior se tiene:
Multiplicamos al segundo miembro por una constante (al numerador y al denominador)
Luego: AC = 12k ; BC = 8k
Reemplazamos en la ecuación (I)
12k + 8k = 40
20k = 40
k = 2
Luego:
AC = 12k = 12 (2) = 24
BC = 8k = 8 (2) = 16
Eso es todo, espero que puedas entender. No te olvides valorar la respuesta
1 respuesta más de otro experto
·
·
¡Hola Carolina!
De nuevo usaremos el teorema de la bisectriz.
En un triángulo, la razón entre dos lados es igual a la razón de las partes en las que queda dividido el tercer lado por la bisectriz de ángulo interno opuesto.
El lado AB mide 12+8=20 cm
Luego conociendo el perímetro, entre los otros dos medirán
$$\begin{align}&AC+BC = 60 - 20 = 40\\&\\&AC=40-BC\\&\\&\text{Y aplicando el teorema de la bisectriz}\\&\\&\frac{AC}{BC}=\frac{12}{8}\\&\\&8AC=12BC\\&\\&\text{Ahora sustituimos AC}\\&\\&8(40-BC)= 12BC\\&\\&320 - 8BC = 12BC\\&\\&320= 20BC\\&\\&BC= \frac {320}{20}=16\,cm\\&\\&AC=40-BC = 40-16=24\, cm\end{align}$$.
: