¿Cómo determino las asíntotas de una función?

·

·

¡Hola Francisco!

Hay tres clases de asíntotas.

Verticales, cuando la función tiende a infinito para un valor finito de x. Uno de los ejemplos más claros es cuando el denominador vale 0 y el numerador no.

En esta función para x=-1 se hace 0 el denominador pero el numerador no.

Luego tenemos la asíntota vertical cuya ecuación es x=-1

·

Horizontales cuando el límite en -inifinito o + infinito es un númer finito. Ten en cuenta que pueden ser dos asíntotas distintas si los limites en - infinito y + infinito son distintos.

En este caso el limite en +infinito es +infinito, y el límite en -infinito es -infinito, como no son límites finitos no hay asíntotas horizontales.

· Oblicuas cuandola función en -infinito o -infinito tiende a una recta que no es vertical ni horizontal. Si en uno de los infinitos hay asíntota horizontal no puede haberla oblicua.

La fórmula para calcular las oblicuas es:

y=mx+m

Para calcular m hacemos:

$$\begin{align}&m=\lim_{x\to \pm\infty}\frac {f(x)}x\end{align}$$

Esa m es la pendiente de la asíntota, si m es un número finito distinto de 0 existe asíntota oblicua y continuamos.  Recordar que se deben calcular límites en los dos infinitos, ya que algunas veces pueden ser distintos.

Y si m es finito y distinto de 0 vamos acalcular b

$$\begin{align}&b=\lim_{x\to\infty} \left(f(x)-mx\right)\end{align}$$

En nuestra fúnción el cálculo es así:

$$\begin{align}&m=\lim_{x\to\pm \infty}\frac{f(x)}{x}=\lim_{x\to\pm \infty}\frac{\frac{x^2+2}{x+1}}{x}=\lim_{x\to\pm \infty}\frac{x^2+2}{x^2+x}=1\\&\\&b=\lim_{x\to\pm\infty}(f(x)-x)=\lim_{x\to\pm\infty}\frac{x^2+2}{x+1}-x=\\&\\&\lim_{x\to\pm\infty}\frac{x^2+2-x^2-x}{x+1}=\lim_{x\to\pm\infty}\frac{2-x}{x+1}=-1\\&\\&\text{Luego la asíntota oblicua es:}\\&\\&y=x-1\end{align}$$

Y esta es la gráfica:

:

:

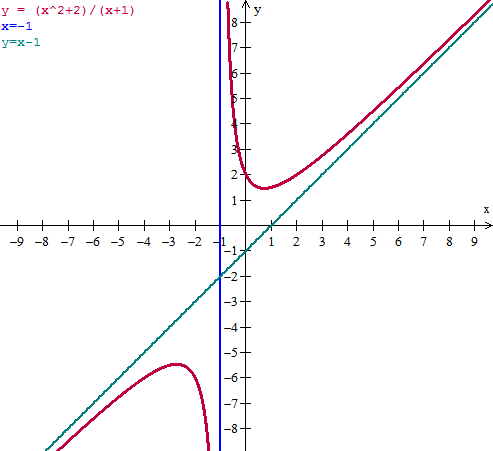
¡Gracias! Profe, valoro muchísimo su apoyo. Profe, disculpe, ¿cuál página es la que utiliza para graficar?