Los conejos están muy libres! En ese caso, la función exponencial esy = 2 x
Supongamos que tenemos un conejo macho y una hembra, y ellos producen cuatro conejitos (supón que dos son machos y dos hembras) que a su vez producen ocho. Y así, con la misma tasa de aumento, la próxima generación producirá 16, la próxima 32, la próxima 64 y así sucesivamente. Claro, estamos suponiendo en este modelo simple que el alimento es infinito y ¡Los conejos están muy libres! En ese caso, la función exponencial es
y = 2 x
O si designamos a C como el número de conejos y a t, como el número de periodos de reproducción de los conejos, se expresaría:
C = 2t
La base es ahora 2. Nota que si t = 1, C = 2 lo que quiere decir que en el momento inicial (en este modelo consideramos el inicio en t=1) se empieza con dos conejos.
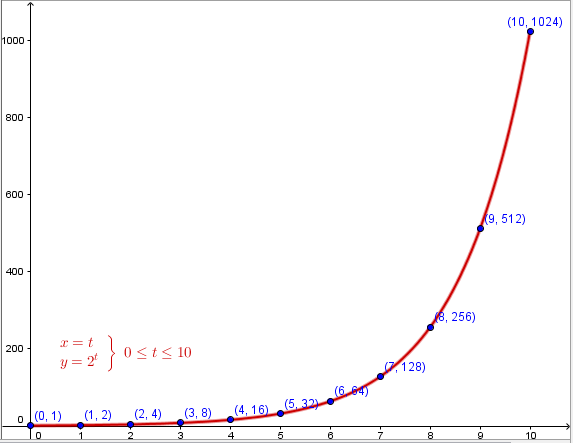
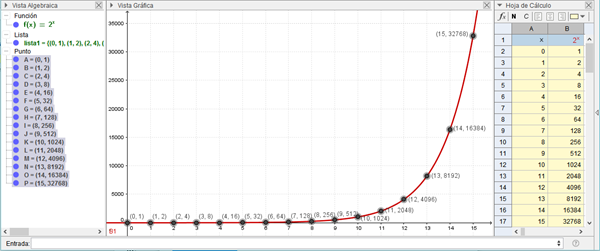
Para esta función de los conejos C = 2t tabula los valores t desde cero hasta 10 de uno en uno, e identifica los números mencionados en el ejemplo del inicio de este ejercicio. Localiza los puntos en una gráfica, o utiliza un software graficador, para ver cómo es la gráfica. Puedes apoyarte del software Geogebra (http://www.geogebra.org/)
2. Menciona qué modelo matemático utilizaste y por qué es el modelo adecuado; además explica ¿de qué forma este modelo matemático te puede ayudar a comprender procesos de variación poblacional?
1 Respuesta
·
·
¡Hola Patricia!
Aparte de la tabla de 0 a 10 de la función he añadido el total de conejos que habrá, no lo piden pero no está de sobra.
Los números que hay que identificar están en la segunda columna, son los 2 conejos iniciales y los 4, 8, 16, 32 y 64 que cita que aumentan en cada generación.
Esta es la gráfica:
2)
Esta pregunta es bastante teórica, depende de lo que ponga en vuestro libro, yo no lo conozco.
El modelo es el exponencial que proviene de:
$$\begin{align}&C(t) = Ae^{kt}\\&\\&\text{Si llamamos }b=e^k \text{ tendremos}\\&\\&C(t)=Ab^t\\&\\&\text{En nuestro caso es }\\&A=1\\&b=2\\&\text{con lo que queda}\\&\\&C(t)=2^t\end{align}$$Es el modelo adecuado porque dando a t el valor de la generación se obtienen los conejos nuevos de esa generación tal como vimos al hacer la tabla.
Ayuda porque describe más o menos lo que pasa con las poblaciones de conejos, asi te pudes hacer una idea de cuantos conejos nacerán en determinada generación y mediante sumas se puede saber cuántos conejos habrá en total si no se retira ninguno.
Eso es lo que pienso yo, si en el libro os viene una respuesta más apropiada la pones.
:
:
La gráfica de Geogebra se ha hecho con la orden
Curve[t, 2^t, t, 0, 10]
La primera parte es t, siginifica la ecuación paramétrica en el eje X
La segunda 2^t es la ecuación paramétrica en el eje Y
La tercera t es por ser la variable paramétrica.
0 es el límite inferior
10 es el límite superior.
Haré aquí la tabla y gráfica para 15 generaciones, lo haré todo con Geogebra ya que tiene hoja de Cálculo.
Esta es la imagen:
Y este es el fichero de Goegebra: Conejos hasta 15 generaciones
Y eso es todo, saludos.
:
:
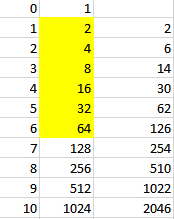
[email protected] - jose vazquez
No se como hacerla, estudiamos en línea y no nos enseñan como ya vi tutoriales pero encuentro como - cris zamora
Cris Zamora, escribe Curve[t, 2^t, t, 0, 10] en la caja de abajo donde se ponen líneas de órdenes. - Valero Angel Serrano Mercadal
En qué programa puedo hacer la gráfica? - ITZEL Alt
ITZEL. La he hecho con el programa Geogebra que aparece citado precisamente en el enunciado con el enlace de descarga. Es un programa sencillo pero no tanto. - Valero Angel Serrano Mercadal
como le hiciste para que las ordenadas empiecen desde el 200? - Karina rey
¡Hola Karina! En Opciones se pueden elegir las medidas de los ejes y la proporción entre ellos. Hay una forma aun más fácil de encoger o agrandar un eje. Teniendo elegida la opción de mover en el último icono de arriba te pones sobre un eje pinchas y arrastras con lo cual harás que ese eje sea más grande o más pequeño. - Valero Angel Serrano Mercadal
Muchas gracias!! - Karina rey
muchas gracias profe ya me salio solo quiero poner las cantidades en los puntos como usted, como lo hizo - cris zamora
Pincha en el primer icono, el de elige y mueve. Luego pincha donde pone punto del cuadro de vista algebraica, de modo que queden seleccionados todos los puntos. Pincha con el botón izquierdo y pulsa en propiedades. En la ventana que se abre, en la pestaña básico, en donde pone etiqueta visible despliega y pincha en valor. Luego cierra las propiedades. - Valero Angel Serrano Mercadal
mestro, no entiendo... ¿dónde se colocan los valores? Porque si me sale la gráfica pero no me da los valores... ¿se tiene que hacer primero una tabla? ¿O cómo se colocan los valores? - Guillermo Navarro
Los puntos los debes poner uno por uno escribiéndolos en la línea de abajo. Luego haz lo que decía en el comentario anterior para que salgan las coordenadas. - Valero Angel Serrano Mercadal
Buenas noches....estoy batallando para unir los puntos. ¿Cómo puedo hacerlo? y la otra pregunta, que opción uso para escribir el texto dentro de la gráfica? es decir, x=t y= 2t, etc. Gracias de antemano por la ayuda. - PeAr JeMa
Buenos días, ya he resuelto el problema de unir los puntos. Solo me gustaría saber si en cuanto a la segunda pregunta que he hecho ( que opción uso para escribir el texto dentro de la gráfica? es decir, x=t y= 2t, etc.) si éste ¿lo puedo escribir fuera de la gráfica? Muchas gracias!! - PeAr JeMa
A mí no me sale así, mi gráfica empieza a partir del 1 aún cuando pongo esa fórmula que usted escribe. No entiendo!! :( - route boutique
Route. Curve[t, 2^t, t, 0, 10] El parámetro de comienzo de la función es 0, ahí debe empezar la gráfica, si acaso puede pasar que se confunda con el eje X, pero si le das otro color tiene que aparecer. - Valero Angel Serrano Mercadal
PeAr JeMa. Debes pinchar en la función y en propiedades, en la pestaña básico elegir que se vea el valor de la función. - Valero Angel Serrano Mercadal
Buenos días. Quisiera me ayudara a aclarar lo siguientes comentarios del tutor... Aspectos de mejora:- 1.- En la tabulación el número total de conejos por cada generación se obtiene al calcular 2t, no se requiere realizar alguna otra operación.2.- Es necesario etiquetar los ejes, es decir, indicar que en eje X se ubica los periodos y en eje Y el total de conejos.3.- Es necesario precisar cómo el modelo exponencial permite entender los procesos de variación. ¿pero por qué el modelo es adecuado? Es necesario profundizar en el estudio de este tipo de función, para observar cómo interviene en el análisis de variación de poblaciones. - PeAr JeMa
¡Hola PeAr! La tercera columna es el número total de conejos. Si el tutor no la quiere quítala, yo la consideré interesante, pero si no le gusta la quitas. Pues etiqueta los ejes, si lo haces conb Geogebra tiene la opción de añadir texto. O puedes editar la imagen con el Paint de Windows y añadir texto también. Asimismo en la tabulación también puedes poner en el encabezado los ejes y lo que significan, en el eje X va el tiempo o generación (no sé que le gustará más al tutor) y el el eje Y va el número de conejos nuevos de cada generación. Lo que dices en el punto 3 es necesario tener la teoría específica y copiarla para contestar como a él le gusta. - Valero Angel Serrano Mercadal
Comentario borrado por el autor - PeAr JeMa
Valero Angel Serrano Mercadel. Perdoneme, corrijo.... eje vertical como y= número de conejos y eje horizontal como x= generación de conejos. ¿Así es correecto como estoy entendiendo el caso del punto numero dos con referencia a los ejes? Gracias !! - PeAr JeMa
El nombre completo en el eje Y sería: número de conejos nuevos en la generación x, lo cual es muy largo, yo lo dejaría en número de conejos nuevos. - Valero Angel Serrano Mercadal
Muchas gracias Sr. Valero. - PeAr JeMa
¡Gracias, Maestro! Agradezco la manera tan clara con la que explica los problemas y los ejemplos para estos temas algo complicados. - Patricia Eaton