Dos problemas de matemática: Conteo
1. Dados los conjuntos A = {1, 2, ...,6} y B = {1, 2,...,10}, ¿cuántas funciones estrictamente crecientes f : A → B pueden definirse? ¿cuántas además cumplen que f(4) = 7?
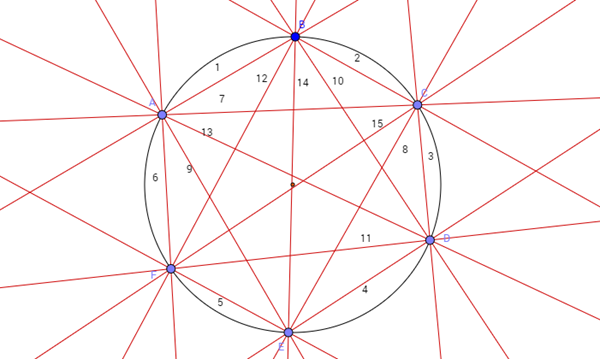
2. Dados seis puntos sobre una circunferencia, se trazan todas las cuerdas que estos puntos definen. ¿Cuál es la probabilidad de que al escoger aleatoreamente cuatro de estas cuerdas se forme un cuadrilátero convexo?
2 respuestas
·
·
¡Hola Jaime!
Debe ser un ejercicio en cada pregunta. Contestaré el primero.
En cualquier conjunto de 6 elementos del conjunto imagen hay una única forma de que la función sea estrictamente creciente, asignando a f(19 el menor valor de los 6, a f(2) el segundo, etc.
Luego habrá combinaciones de 10 tomadas de 6 en 6 funciones estrictamente crecientes
C(10,6) = 10·9·8·7 / (4·3·2·1) = 5040 / 24 = 210
·
Si f(4)=7 tendremos por una parte que f(1), f(2) y f(3) tendrán como valores posibles 1,2,3,4,5,6 siempre en orden creciente. Y f(5) y f(6) podrán valer 8,9 ó 10 también siempre en orden creciente. Esto será
C(6,3) · C(3,2) = [6·5·4/(3·2·1)] · [3·2/(2·1)] = (120/6)·(6/2) = 20·3=60
Y eso es todo, manda el otro ejercicio en otra pregunta. Aunque ahora tengo que dejar el ordenador algunas horas.
Saludos.
:
:
Vamos con el segundo ejercicio.
Veamos cuántas cuerdas habrá.
Cada punto se puede unir con otros 5, luego habría 6·5 = 30 pares ordenados con principio y final.
Pero cada cuerda corresponde a dos pares ya que el par (a, b) y el (b, a) son la misma cuerda. Luego como cada cuerda tiene dos pares ordenados, el número de cuerdas es la mitad de los pares ordenados
30/2 = 15
Entonces los casos posibles serán combinaciones de 15 tomadas de 4 en 4
C(15,4) = 15·14·13·12 / (4·3·2·1) = 1365
Ahora viene lo difícil, elegir cuáles de esas combinaciones definen un polígono convexo.
El polígono convexo se define por sus cuatro vértices, hay una única forma de unirlos con aristas para que salga convexo, si empezamos por el de menor numeración la primera arista irá al de segunda numeración, la segunda al de tercera numeración, la tercera al de cuarta numeración y de este al vértice primero.
Los cuatro vértices son combinaciones de 6 tomadas de 4 en 4
C(6,4) = C(6,2) = 6·5/2 = 15
Luego ese el número de cuadriláteros convexos qus se pueden formar
Y si sus vértices ordenados son (v1, v2, v3, v4) las cuerdas que lo forman son (v1, v2), (v2, v3), (v3, v4) y (v4, v1)
Y la probabilidad serán las elecciones que dan cuadrilátero convexo entre todas las elecciones posibles
P=15/1365 = 1/91 = 0.010989010989(010989)...
:
:
Intentaré echar un poco de luz sobre el 2° ejercicio.
Sobre 6 puntos no alineados tenemos que de cada punto, podemos unirlas con cada uno de los 5 puntos restantes, por lo que tendremos 6*5 = 30 rectas posibles, el tema es que al hacer esto estamos contando cada recta 2 veces ya que la contamos del punta A al punto B, pero la volvemos a contar del punto B al punto A, así que para saber cuantas rectas tenemos, al resultado anterior hay que dividirlo por 2, teniendo una cantidad de 15 rectas posibles.
Como segundo paso tenemos que ver de cuantas formas podemos tomar 4 rectas, entre las 15 dadas y esto lo da la combinatoria (15,4) cuyo valor es 1365 formas posibles de elegir 4 rectas
El tercer paso sería ver de esas formas posibles, cuales forman un cuadrilátero convexo
Antes de eso veamos una imagen de ejemplo, donde las letras indican los vértices y los números de 1 a 15 las rectas en cuestión
A partir de esa imagen, intentá calcular cuantos cuadrilateros convexos hay... yo te dejo brevemente y luego lo continúo...