El número de viviendas construidas por año, N, depende de la tasa de interés hipotecaria r de acuerdo con la fórmula:
El número de viviendas construidas por año, N, depende de la tasa de interés hipotecaria r de acuerdo con la fórmula:
$$\begin{align}&𝑁(𝑟) = \frac{50}{100+r^2}\end{align}$$Donde N está en millones. La tasa de interés actualmente está en 12% y se predice que disminuirá a 8% en los siguientes 2 años de acuerdo con la fórmula
$$\begin{align}&r(t)=12- \frac{8t}{t+24}\end{align}$$Donde t es el tiempo medido en meses, a partir de ahora. Exprese N como una función del tiempo t. Calcule el valor de N cuanto t=6.
1 respuesta
Respuesta de Valero Angel Serrano Mercadal
1
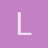
 En la Segunda parte no quedaría como 116t^2 en vez de 16t^2?
En la Segunda parte no quedaría como 116t^2 en vez de 16t^2?