Calcular el área de una figura.
Calcule el área de la figura sabiendo que:
$$\begin{align}&\int_b^d \! F(x) \, \mathrm{d}x = 2\\&\\&\int_d^c \! F(x) \, \mathrm{d}x = 0,8 \\&\\&\int_a^b \! F(x) \, \mathrm{d}x = \int_b^c \! F(x) \, \mathrm{d}x \end{align}$$¿Cuanto vale...?
$$\begin{align}&\int_a^d \! F(x) \, \mathrm{d}x\ \end{align}$$¿Por qué la diferencia?
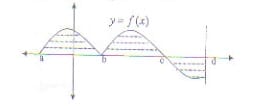
Las respuestas son: 6,4 y 4,8
2 Respuestas
Respuesta de Lucas m
1
;)
Hola Maar!
El área es la suma del área de los tres recintos
Como las integrales entre a y b; y b y c son iguales esos dos recintos tiene igual área
$$\begin{align}&Area=2 \int_a^bF dx+ \Bigg|\int _c^d F dx \Bigg |\\&\end{align}$$Entre c y d la función es negativa luego el área es el valor absoluto de la integral
Recuerda que al intercambiar los límites de integración la integral cambia de signo
$$\begin{align}&\int_c^d Fdx<0 \Rightarrow A=- \int_c^d Fdx=\int_d^c Fdx\\&\\&2= \int_b^c Fdx+ \int_c^d Fdx\\&\\&2= \int _b^c F dx-\int_d^c Fdx\\&\\&2=\int_b^c Fdx-0,8\\&\\&\Rightarrow\\&\\&\int_b^c Fdx=2,8\\&\\&\Rightarrow\\&Area= 2 \int_a^b Fdx + \int_d^c F dx=2(2,8)+0,8=6,4\\&\\&\end{align}$$Saludos
;)
;)
Respuesta de Valero Angel Serrano Mercadal
1
·
·
¡Hola Maar!
Haremos uso de las prpiedades de las integrales, de estas dos
$$\begin{align}&\int_a^b f(x)\,dx+\int_b^c f(x)\,dx=\int_a^c f(x)\,dx\\&\\&\int_a^b f(x)\,dx=-\int_b^af(x) dx\\&\\&\\&Entonces\\&\\&\int_b^cF(x)\,dx+\int_c^dF(x)\,dx=\int_b^dF(x)\implies\\&\\&\int_b^cF(x)\,dx=\int_b^dF(x)-\int_c^dF(x)\,dx\implies\\&\\&\int_b^cF(x)\,dx=\int_b^dF(x)+\int_d^c F(x)\,dx=2+0.8=2.8\\&\\&\int_a^b F(x)\,dx=\int_b^c F(x)\,dx=2.8\\&\\&\text{Y ahora}\\&\\&A=\bigg|\int_a^b F(x)dx\bigg|+\bigg|\int_b^cF(x)dx\bigg|+\bigg|\int_c^d F(x)dx \bigg|=\\&\\&2.8+2.8+0.8=6.4\end{align}$$Y eso es todo, saludos.
:
: