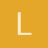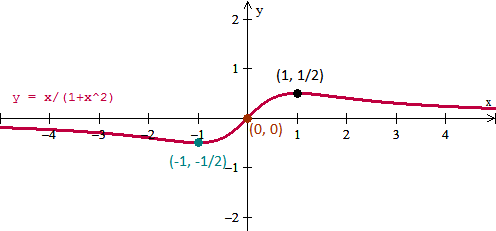Dibujar la gráfica de la ecuación y= x/(x^2+1) . Identificar las intersecciones con los ejes y buscar las simetrías

El rango, el dominio, asíntotas y oblicuas.

El dominio es todo R. Al ser un cociente de polinomios únicamente no habría dominio donde el denominador fuera 0.

Pero

x^2+1 = 0

No tiene soluciones reales

El rango será el dominio de la función inversa.

$$\begin{align}&y = \frac x{x^2+1}\\&\\&yx^2 + y = x\\&\\&yx^2-x+y=0\\&\\&x=\frac{1\pm \sqrt{1-4y^2}}{2y}\\&\\&\text{El dominio de la inversa debe cumplir}\\&\\&1-4y^2\ge 0\\&\\&4y^2\le 0\\&\\&y^2 \le \frac 14\\&\\&|y| \le \frac 12\\&\\&-\frac 12 \le y \le \frac 12\\&\\&Rango\; f=\left[-\frac 12, \frac 12\right]\\&\\&\text{Y los puntos donde se alcanzan estos valores mínimo y minimo son}\\&\\&x_{mín}=\frac{1\pm \sqrt {1 -4 \left(-\frac 12\right)^2}}{2\left(-\frac 12\right)}=\frac{1\pm0}{-1}=-1\\&\\&x_{máx}=\frac{1\pm \sqrt {1 -4 \left(\frac 12\right)^2}}{2\left(\frac 12\right)}=\frac{1\pm0}{1}=1\\&\\&\text{Luego tenemos los puntos}\\&\\&\left(-1, -\frac 12\right)\quad \left(1, \;\frac 12\right)\end{align}$$

Las interseccines con los ejes son:

Con el eje X allá donde el numerador sea 0, luego en x=0, por tanto el punto (0,0)

Y con el eje Y es el mismo corte por lo tanto.

No hay asíntotas verticales porque en ningún punto real la función se ha ce infinito

Hay asíntotas horizontales (una sola en realidad) porque el límite de la función tanto en -ifinito como en infinito es 0. Luego la recta x=0 es asíntota horizontal.

Al haber horizontal no hay oblícuas.

Respecto a las simetrías tenemos una simetría central, respecto al punto (0, 0) ya que

f(-x) = -f(x)

$$\begin{align}&f(-x)=\frac{-x}{1+(-x)^2}=-\frac{x}{1+x^2}=-f(x)\end{align}$$

Y esos son los datos que me dices se pueden utilizar, con ello y algunos puntos más que puedas calcular la gráfica es así:

:

:
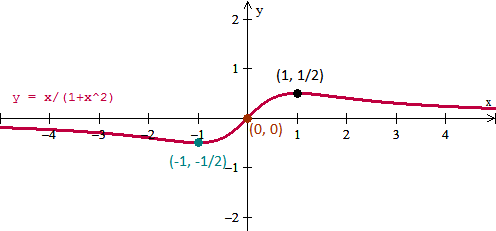