Ejercicios de probabilidad está discriminado en la siguiente tabla
Alguien me puede explicar o mostrar un ejemplo de como resolver los siguientes ejercicios.
El número de casas en una ciudad a los que su avalúo es el adecuado está discriminado en la siguiente tabla:
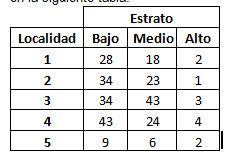
1. ¿Cuál es la probabilidad de encontrar una casa con adecuado avalúo del estrato bajo dado que es de una región inferior o igual a 3?____________
2. Se podría decir que de cada 1000 casas de una región inferior o igual a 3 ________ casas son de estrato bajo.
3. La probabilidad de encontrar una casa con adecuado avalúo de la región 5 y de estrato medio es _________
Cordial saludo
1 respuesta
·
·
La probabilidad es el cociente entre los casos favorables y los casos posibles.
1) Buscamos la probabilidad de un avalúo del estrato bajo cuando la región es inferior o igual a 3.
Calculamos los casos favorables que son los avaluos de estrato bajo en las regiones 1,2 y 3
casos favorables = 28+34+34 = 96
Y los casos posibles son todos los avalúos de esas tres regiones. A los ya sumados sumamos los avalúos medios y altos de esas tres regones
casos posibles = 96+18+23+43+2+1+3 = 186
Luego la probabilidad es
p = 96/186 = 16/31 = 0.5161290323
·
2)
El tanto por mil, que es como se llamaría a esa cantidad se obtiene multiplicando la probabilidad por mil
1000 · 0.5161290323 = 516.1290323
Si solo se quiere decir un número entero sería 516
·
3)
Volvemos a lo hecho en el apartado 1, serán los casos favorables entre los posibles. Ahora es más sencillo porque solo se tienen en cuenta los de la región 5
Casos favorables = avalúos de estrato medio en la región 5 = 6
Casos posibles = 6+9+2 = 17
Luego la probabilidad es
p = 6/17 = 0.3529411765
·
:
:
Hola!!!
Esto es resuelto con el teorema de bayes?
No, simplemente se usa la fórmula de la probabilidad condicionada.
$$\begin{align}&P(A|B)=\frac{P(A\cap B)}{P(B)}\\&\\&\text{Por ejemplo:}\\&\text{A=ser una casa avaluada del estrato bajo}\\&\text{B=ser de una regíón inferior o igual a tres}\\&\\&P(A|B)=\frac{\frac{\text{avaluos de estrato bajo de regiones 1,2y3}}{\text{avalúos totales}}}{\frac{\text{avalúos de las regiones 1,2 y 3}}{\text{avalúos totales}}}=\\&\\&\frac{\text{avaluos de estrato bajo de regiones 1,2y3}}{\text{avalúos de las regiones 1,2 y 3}}\end{align}$$que es la forma en que lo calculamos.
Saludos.
:
:
