¿ Como resuelvo este ejercicio de funciones?
Describe en unas líneas el comportamiento de la función (crecimiento, decrecimiento, máximos/mínimos).
2 respuestas
·
·
¡Hola Elsepu!
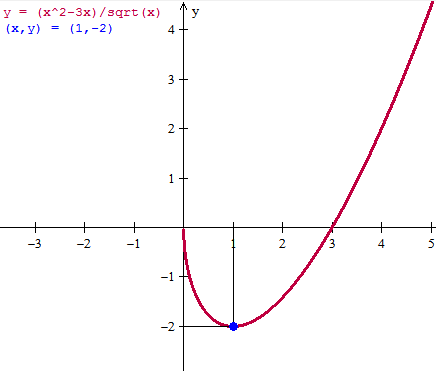
Primero vemos que el dominio es (0, infinito) ya que el radicando debe ser no negativo y tampoco puede ser 0 por estar en el denominador.
Es interesante saber que el límite cuando tiende a 0 es 0, es fácil calcularlo simplificando numerador y denominador.
Corte con el eje Y no tiene aunque tiende a 0. Y veamos si corta al eje X
x^2-3x=0
x(x-3)=0
x=0 no sirve
x-3=0
x=3
Luego corta al eje X solo una vez en x=3
Para calcular derivadas lo mejor es simplificar antes.
$$\begin{align}&f(x) =\frac{x^2-3x}{\sqrt x}=\frac{x^2-3x}{x^{\frac 12}}=x^{\frac 32}-3x^{\frac 12}\\&\\&\text{derivamos e igualamos a 0}\\&\\&f'(x)=\frac 32 x^{\frac 12}-\frac 32x^{-\frac 12}=0\\&\\&\text{multiplicamos por }x^{\frac 12}\\&\\&\frac 32 x-\frac 32=0\\&\\&x-1 =0\\&x=1\\&\\&\text{calculamos la derivada segunda}\\&\\&f''(x)=\frac 34x^{-\frac 12}+\frac 34x^{-\frac 32}\\&\\&f''(1)=\frac 34+\frac 34=\frac 32\gt0\implies mínimo\\&\\&\text{luego el mínimo es }(1,f(1))=(1,-2)\\&\\&\text{Y los intervalos}\\&\\&(0,1)\quad\; decreciente\\&(1,\infty)\quad creciente\end{align}$$Esta es la gráfica:
Y eso es todo, saludos.
:
:
Yo no calculé el signo de la derivada, pero lo deduje en base a que la función es continua y tiene un único punto crítico que es mínimo relativo. Entonces todo lo anterior al mínimo es decreciente y todo lo posterior creciente.
;)
;)
Hola elsepu!
Esta función esta definida para x>0
$$\begin{align}&\lim_{x \to 0^+}\frac{x^2-3x}{\sqrt x}=\frac{0}{0}=\lim_{x \to 0^+}\frac{x(x-3)}{x^{\frac{1}{2}}}=\lim_{x \to 0^+}x^\frac{1}{2}(x-3)=0\\&\\&\\&\lim_{x \to + \infty}\frac{x^2-3x}{\sqrt x}=\frac{+ \infty}{+\infty}=\lim_{x \to +\infty}x^\frac{1}{2}(x-3)=+ \infty\\&\\&Cortes \ eje \ X : y=0=\frac{x^2-3x}{\sqrt x} \Rightarrow x^2-3x=0 \Rightarrow x(x-3)=0 \Rightarrow x=3\\&\\&Crecimiento: Derivando\\&\\&y'=\frac{(2x-3) \sqrt x -(x^2-3x) \frac{1}{2 \sqrt x}}{(\sqrt x)^2}=\frac{(2x-3)2x-(x^2-3x)}{2x \sqrt x}=\\&\\&=\frac{4x^2-6x-x^2+3x}{2x \sqrt x}=\frac{3x^2-3x}{2x \sqrt x}\\&\\&y'=0\Rightarrow \frac{3x^2-3x}{2x \sqrt x}=0 \Rightarrow 3x(x-1)=0 \Rightarrow x=1\\&\\&intervalos \ crecimiento:\\&(0,1) \Rightarrow f'( \frac{1}{2})=3(\frac{1}{4})-\frac{3}{2} <0 \Rightarrow decreciente\\&\\&(1,+ \infty) \Rightarrow f'(10)>0 \Rightarrow creciente\\&\Longrightarrow mínimo \ relativo \ en \ x=1\\&f(1)=\frac{1-3}{\sqrt 1}=-2 \Rightarrow (1,-2)\end{align}$$graficando:
