Regresión y correlación lineal, como resolver?
Para los siguientes datos tomados de una muestra.
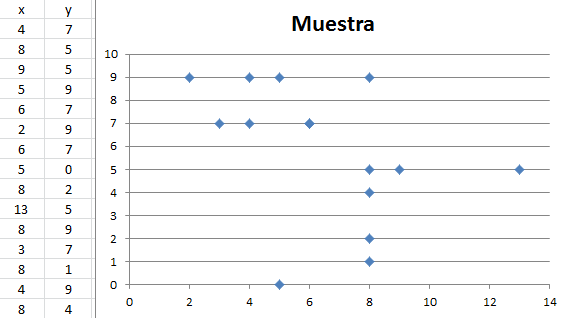
x 4 8 9 5 6 2 6 5 8 13 8 3 8 4 8
y 7 5 5 9 7 9 7 0 2 5 9 7 1 9 4
Determina:
- Elabora el diagrama de dispersión
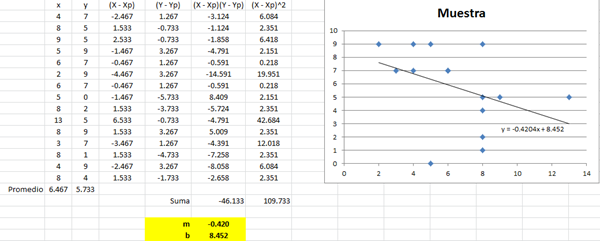
- La ecuación de regresión lineal.
- El coeficiente de correlación y de determinación
- Utilizando la ecuación de regresión lineal, estima para un valor de la variable
x= 12, el valor de la variable “y”
Utilizando la ecuación de regresión lineal, estime para un valor de la variable “y=3” el valor de la variable “x”.
1 Respuesta
¿Lo tenés que hacer "a mano" o mediante un software (ej/ Excel)?
En función de tus comentarios la respuesta puede ser muy simple o "simple pero laborioso" :)
Buenas Tardes!
Lo tengo que hacer a mano, pero no tengo idea de como hacerlo, por más que veo los tutoriales en internet ni las lecturas de la escuela, estoy haciendo mi licenciatura en línea, es por ello que se mecomplica aun más, pero no entiendo .
Ok, el punto 1 si lo tienes que hacer "a mano" pues no hay otra, yo te dejo la imagen pero básicamente deberás marcar tus ejes (X e Y) e ir marcando cada punto en el mismo
La ecuación de regresión lineal (o de mínimos cuadrados) es aquella que minimiza los errores entre los valores dados y una recta. Por como están los datos, se ve que esta recta será cualquier cosa porque los datos no están ni cerca de estar en una recta.
Para entender como hacerlo, si tenés el Excel podés buscar la ayuda de la función ESTIMACION. LINEAL donde te dice como se calculan los parámetros m, b de la ecuación
y = m x + b que representa la recta
Básicamente lo que dice es que:
$$\begin{align}&m = \frac{\sum(x-\overline x)(y-\overline y)}{\sum(x- \overline x)^2}\\&y = \overline y - m \overline x\\&Donde\ \overline x, \overline y\ son\ las\ medias\ muestrales\end{align}$$En este caso
$$\begin{align}&\overline x = 6.46\\&\overline y = 5.73\\&\end{align}$$Esos pasos los voy a hacer en Excel pues es muy trabajoso hacerlo a mano, pero te quedan las tablas (vos sí, deberías hacerlo todo a mano).
Fijate que incluí el gráfico, ahora con la curva de regresión y los parámetros son los mismos que los que calculé yo
y eso seria todo? es decir. el ultimo punto lo haré como una ecuación normal o esta incluido en la ultima tabla que puso?
Ouchs, olvidé esos pasos :)
3)
$$\begin{align}&Tenemos\ que\ y = mx + b\\&y = -0.420 x + 8.452\\&Coeficiente \ de\ Determinación\\&R^2 = \frac{\sum (y^* - \overline y)^2}{\sum(y - \overline y)^2}\\&\text{Donde y}^* \text{ es el valor de y pero usando la recta de mínimos cuadrados calculada}\end{align}$$Calculando esos valores, tenemos que R^2 = 0.1578
$$\begin{align}&\text{El Coeficiente de correlación se define como}\\&\rho = \frac{Cov(X,Y)}{\sigma(X)\cdot \sigma(Y)} = \frac{-3.2952}{2.7997 \cdot 2.9633}=-0.3972\\&\end{align}$$4) si x=12
y = -0.420 * 12 + 8.452 = 3.407
Si y = 3
3 = -0.420 * x + 8.452
-0.420 x = 3 - 8.452
x = -5.452 / (-0.420)
x = 12.981