Geometria analitica. Calculo de areas
- Calcula en cada caso razonadamente el valor de m para que:
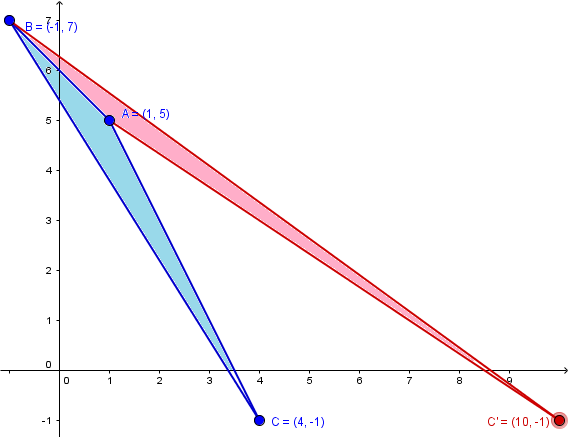
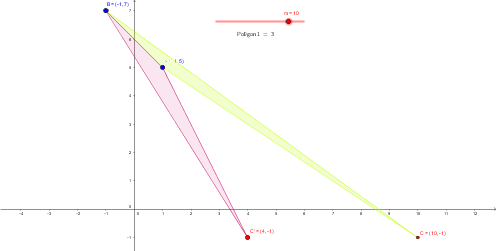
a) Los puntos A(1,5), B(-1,7), C(m,-1) formen un triangulo de área ABC de 3 unidades.
3 Respuestas
·
·
¡Hola Danidvddanydvd!
El área de un triángulo se puede calcular como un medio del módulo del producto vectorial de los vectores formados por dos lados.
Hagamos A el vértice de esos dos vectores:
$$\begin{align}&A(1,5), B(-1,7), C(m,-1)\\&\\&\vec{AB}=B-A=(-2,2)\\&\vec{AC}=C-A = (m-1,-6)\\&\\&\text{Puesto que el producto vectorial es en }\mathbb R^3 \\&\text{añadimos una tercera coordenada nula y }\\&\text{lo calculamos con la fórmula típica del determinante}\end{align}$$| i j k |
| -2 2 0 | = 0i + 0j + [2·6-2(m-1)]k
|m-1 -6 0 |
·
El módulo del vector es
|12-2m+2| = |14 -2m|
Y el área es la mitad
A = |7 - m| = 3
Si consideramos positivo el interior es
7 - m = 3
m=4
Si lo consideramos negativo es
7-m = -3
m=10
Luego hay dos soluciones
m=4
m=10
Y eso es todo, espero que te sirva y lo hayas entendido. Si no es así pregúntame. Y si ya está bien, no olvides valorar las respuestas.
Saludos.
:
:
;)
;) hola danidvddanydvd!!!!
area=b·h/2
Tomaré como base AB, con lo cual la altura será la distancia del vértice C a esta base.
$$\begin{align}&base=|\vec {AB}|\\&\\&\vec {AB}=B-A=(-1,7)-(1,5)=(-2,2) \Rightarrow |\vec {AB}|= \sqrt{2^2+2^2}=\sqrt{8}=2 \sqrt{ 2}=b\\&\\&recta \ r: AB\\&ecuación \ continua\\&\frac{x-x_o}{v_1}=\frac{y-y_o}{v_2}\\&\\&\frac{x+1}{-2}=\frac{y-7}{2} \Rightarrow 2(x+1)=-2(y-7) \Rightarrow x+1=-y+7 \Rightarrow x+y-6=0\\&\\&distancia \ punto (x_0,y_0) a \ recta:Ax+By+C=0\\&h=dist(C,r)=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}=\frac{|m-1-6|}{\sqrt{1^2+1^2}}=\frac{|m-1-6|}{\sqrt{2}}\\&\\&Area=3\\&3=\frac{1}{2}·2 \sqrt 2·\frac{|m-7|}{\sqrt{2}}\\&\\&3=|m-7| \Rightarrow m-7=3 \Rightarrow m=10\\&\\&\Downarrow\\&-3=m-7 \Rightarrow m=7-3=4\end{align}$$Al levantar las barras de valor absoluto hay dos posibilidades.
Asi |x|=3 puede ser x=3 o x=-3
Hay por tanto dos soluciones
Saludos
;)
;)