Hallar "c" correspondiente al teorema de Rolle para:
$$\begin{align}&d)\ f(x)= \sqrt[3] {x} (x-7)^2 \ en \ [0;7]\end{align}$$
2 respuestas
Respuesta de Lucas m
1
;)
Hola Maar!
La función es contnua en ([0,7]
f(0)=0
f(7)=0
luego existe c en (0,7) tal que f'(c)=0
$$\begin{align}&f'(x)=\frac{1}{3 \sqrt[3] {x^2}}(x-7)^2+ \sqrt[3]{x}·2(x-7)=\\&\\&=\frac{(x-7)^2+3 \sqrt[3]{x}\sqrt[3] {x^2}·2(x-7)}{3 \sqrt[3]{x^2}}=\frac{(x-7)^2+6x(x-7)}{3 \sqrt[3]{x^2}}=0\\&\\&x^2-14x+49+6x^2-42x=0\\&\\&7x^2-56x+49=0\\&\\&x_1=1\\&\\&x_2=7\\&\\&c=1\end{align}$$$$\begin{align}&f'(x)=\frac{1}{3 \sqrt[3] {x^2}}(x-7)^2+ \sqrt[3]{x}·2(x-7)=\\&\\&=\frac{(x-7)^2+3 \sqrt[3]{x}\sqrt[3] {x^2}·2(x-7)}{3 \sqrt[3]{x^2}}=\frac{(x-7)^2+6x(x-7)}{3 \sqrt[3]{x^2}}=0\\&\\&x^2-14x+49+6x^2-42x=0\\&\\&7x^2-56x+49=0\\&\\&x_1=1\\&\\&x_2=7\\&\\&c=1\end{align}$$Luego c=1
Al hacer la ecuación no simplifiques el factor (x-7) ya que pierdes la solución buscada
Saludos
;)
;)
Respuesta de Valero Angel Serrano Mercadal
1
·
·
¡Hola Maar!
El teorema de Rolle dice que si f es continua en [a,b] y derivable en (a,b) y f(a)=f(b) entonces existe al menos un punto c en (a,b) fal que f'(c)=0
Veamos si esta función cumple las condiciones
$$\begin{align}&d)\ f(x)= \sqrt[3] {x} (x-7)^2 \ en \ [0;7]\\&\\&\text{f está definida en }[0,\infty)\text{ y es continua en todo él}\\&\\&\text{La derivada es:}\\&\\&f'(x)=\frac 13x^{-2/3}(x-7)^2+2x^{1/3}(x-7)=\\&\\&\frac{(x-7)^2}{3 \sqrt[3]{x^2}}+ 2 \sqrt[3]x(x-7)\\&\\&\text{f' es continua en }(0,\infty)\\&\\&f(0)=0\\&f(7)=0\\&\\&\text{Se cumplen las condiciones}\\&\text{Y vamos a ver que es verdad}\\&\\&f'(x)=\frac{(x-7)^2}{3 \sqrt[3]{x^2}}+ 2 \sqrt[3]x(x-7)=0\\&\\&\text{La respuesta no puede ser x=0 luego se puede }\\&\text{multiplicar por x y expresiones que serán distintas de 0}\\&\\&\text{Multiplicamos por } 3 \sqrt[3]{x^2}\\&\\&(x-7)^2+6(x-7)x=0\\&\\&(x-7) (x-7+6x)=0\\&\\&\text{x=7 es otra solución, pero tampoco sirve}\\&\\&x-7+6x=0\\&\\&7x = 7\\&\\&x=1\end{align}$$Luego el valor c del que habla el teorema es c=1
Esto gráficamente es que existe un punto donde la tangente es horizontal.
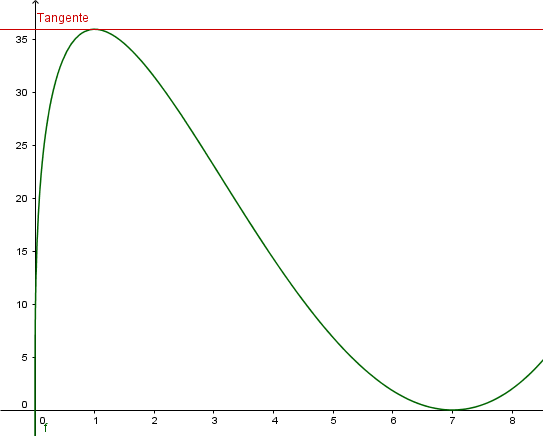
Los ejes tienen que estar desfigurados por fuerza para que la gráfica tenga un tamaño razonable. Dentro de la desfiguración esta gráfica es lo más real posible.
Y eso es todo, saludos.
:
: