¿Me podrían realizar esto de las funciones de matemáticas? (3 parte)

;)

Hola jesusgpe!

Este ejercicio está preparado para hacerlo a partir de las transformaciones gráficas.

Transformaciones:

Si tienes una función  y= f(x)

y=f(x)+k  la gráfica se traslada en vertical: hacia arriba si  k>0

                                                                              hacia abajo si  k< 0

Así en tu caso si :

$$\begin{align}&f(x)=3x^2 \Rightarrow V=(0,0)\\&\\&y=3x^2+4 \  \ \ es \ \ \ y=f(x)+4\end{align}$$

traslación vertical hacia arriba ===> V=(0,4)    la verde

$$\begin{align}&y=3x^2-4 \Rightarrow y=f(x)-4\end{align}$$

traslación vertical hacia abajo ===> V=(0,-4)   la  lila

Si la transformación es tipo y=f(x+k) la gráfica se traslada en horizontal:

si k<0  hacia la derecha

si k>0 hacia la izquierda

c) En tu caso:

$$\begin{align}&y=3(x-1)^2+4 \Rightarrow y=f(x-1)+4\end{align}$$

===> traslación horizontal a la derecha de 1 unidad; y vertical hacia arriba de 4 unidades

V(1,4)   la azul

d)

$$\begin{align}&y=3(x+2)^2-4 \Rightarrow y=f(x+2)-4\end{align}$$

f(x+2) ===> traslación horizontal a la izquierda de 2 unidades

f(x+2)-4    y  de  4 en vertical hacia abajo  ===> V=(-2,-4)      la dorada

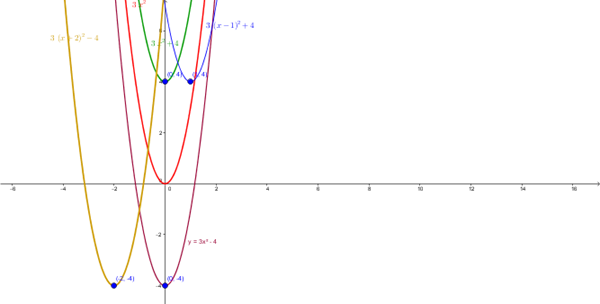
La otra manera de hacerla es a partir de una tabla de valores y buscando el vértice con la fórmula  x=-b/2a       y=ax^2+bx+c

Saludos

;)

;)

·

·

¡Hola Jesusgpe!

Todas estas funciones tienen la forma

f(x)= 3(x-a)^2 + b

En el punto x=a la función tendrá su valor mínimo ya que la parte

3(x-a)^2 será 3(a-a)^2 = 0

que es el mínimo valor que puede tomar, además el valor en x=a es

y= 0 + b = b

Luego el mínimo de la función estará emn el punto

(a, b)

Tratándose de parábolas ese punto será el vértice de la parábola. Y la forma de todas ellas es la misma, salvo que estan trasladadas de modo que el vértice esté es (a, b)

Y eso es todo, saludos.

:

: