Contar el número de triangulo en un polígono convexo de n lados
Un polígono convexo de n lados es tal que no hay punto común alguno para cualesquiera tres de sus diagonales. Determine el número de triángulos que se forman de manera tal que dos de sus vértices sean vértices del polígono y el tercero sea una intersección de dos diagonales.
1 Respuesta
·
·
¡Hola Jaime!
Primero veamos cuántas diagonales hay.
Desde cada vértice puedes mandar una diagonal a cualquier otro punto excepto a si mismo y a los dos vértices contiguos, lu ego podrías mandar diagonales a n-3 puntos.
Esto nos daría n(n-3), pero cada diagonal está contada dos veces ya que aparece cuando va de A a C y cuando va de C a A, luego hay que dividir por 2
Diagonales = n(n-3)/2
Y ahora veamos cuantos puntos deteminan estas diagonales. Cada diagonal corta dentro del polígono a las que no tienen ninguno de los extremos de esta. Las que tienen el extremo A son n-3, las que tienen el extremo C son otras n-3 pero la AC está repetida, luego las que no corta son n-3+n-3-1 = 2n-7. Por tanto las que corta son
n(n-3)/2 - (2n - 7)
Luego el número de cortes será
[n(n-3)/2]·[n(n-3)/2 - 2n + 7] / 2
Ese 2 al final está porque cada punto lo habíamos contado dos veces al estar en dos diagonales.
Y de cada punto de estos podemos lanzar dos lados a vértices del polígono salvo a los dos extremos de la diagonal primera que determinó ese punto y la diagonal segunda
Entonces desde un punto de intersección de diagonales podemos formar
C(n,2) - 2 = n(n-1)/2 - 2 triángulos
Y por lo tanto el número total de triángulos será:
$$\begin{align}&T=\frac{\frac{n(n-3)}{2}·\left(\frac{n(n-3)}{2}-2n+7\right)}2·\left(\frac{n(n-1)}{2}-2 \right)=\\&\\&\frac{n(n-3)·[n(n-3)-4n+14]·[n(n-1)-4]}{16}=\\&\\&\frac{(n^2-3n)(n^2-7n+14)(n^2-n-4)}{16}\\&\\&\text{Y es mejor dejarlo así, cuesta menos operar}\\&\text{esto que el polinomio que saldrá de grado 6}\\&\\&\text{Probemos con n=4, tienen que salir 4}\\&\\&\frac{(16-12)(16-28+14)(16-4-4)}{16}=\\&\\&\frac{4·2·8}{16}=\frac{64}{16}=4\end{align}$$Y para el pentágono hacemos el dibujo
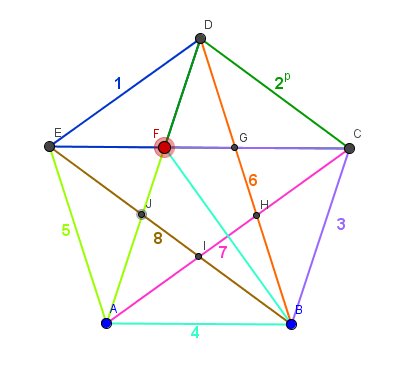
He dibujado solo los triángulos con vértice en F, he numerado los lados opuestos a F, son 8 triángulos, luego si hiciéramos los de F, G, H, I, J serían 5·8 = 40 triángulos.
Veamos lo que diría la fórmula
(25-15)(25-35+14)(25-5-4)/16 = 10·4·16/16 = 40
Oye, parece que va bien.
Y eso es todo saludos.
:
:
$$\begin{align}&\int_0^1 arccos(1-x)dx=\\&\\&t=1-x\implies dt=-dx\\&\\&=-\int_1^0arccos\,t\;dt=\int_0^1arccos\;t\;dt=\\&\\&u=arccos\;t\quad\quad du=- \frac{dt}{\sqrt{1-t^2}}\\&dv=dt\qquad\qquad v=t\\&\\&=t·arccos\;t\bigg|_0^1+\int_0^1 \frac{t}{\sqrt{1-t^2}}dt=\\&\\&1·0-0·\frac{\pi}{2}-\sqrt{1-t^2}\bigg|_0^1= 0-0-0+1=1\\&\\&\text{La probabilidad de cortar será:}\\&\\&P= \frac{1}{\frac{\pi}{2}}= \frac 2\pi\\&\\&\text {luego}\\&\\&\frac{cortan}{tirados}= \frac 2\pi\\&\\&\pi=\frac{2·tirados}{cortan}\\&\\&\\&\\&\end{align}$$Esto no tiene que ver ya lo sé, es que necesito poner esas fórmulas con LATEX.
