Matemáticas - Demostrar relación entre cuerdas y tangentes de circunferencias
Demostrar que dadas dos circunferencias que se intersecan, la recta que contiene a una cuerda en común a ambas circunferencias, biseca a las tangentes comunes a ambas circunferencias
1 respuesta
·
·
¡Hola Fred!
Para contestar ewsta pregunta habría que saber lo que estás estudiando exactamente. No tiene nada que ver si estas estudiando geometría analíca o geometría proyectiva.
Voy a suponer que es estudiado lo que es la potencia de un punto respecto a una circunferencia, que es el producto de las distancias del punto a los dos puntos de corte a la circunferencia por una recta que pasa por el punto y la circunferencia.
Se da la maravillosa propiedad de que la potencia es independiente de la recta que tracemos por lo que la potencia es un valor único. Y también se puede calcular cuando la recta es tangente, en este caso la fórmula es el cuadrado de la distancia.
Entonces, si conoces eso vas a ver que es sencillísimo.
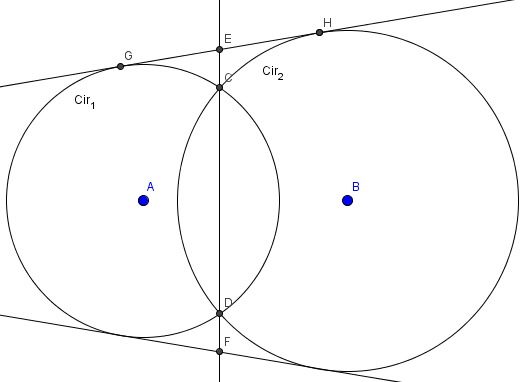
La potencia del punto E respecto a las circunferencias c y d es la misma ya que será
$$\begin{align}&P(E,Cir_1)=P(E,Cir_2)=\overline{EC}·\overline{ED}\\&\\&\text{Y si calculamos la potencia or la recta de la tangente será}\\&\\&P(E,Cir1)=\overline{EG}^{\;2}\\&\\&P(E,Cir2)=\overline{EH}^{\;2}\\&\\&\text{como son iguales}\\&\\&\overline{EG}^{\;2}= \overline{EH}^{\;2}\\&\\&\overline{EG}= \overline{EH}\end{align}$$Con el punto F se hace igual.
:
:
Gracias por tu respuesta y una disculpa si faltó aclarar más la pregunta, la materia es Geometría, y el tema es propiedades de la circunferencia, donde se ven las rectas y los ángulos de la circunferencia, por lo que los puntos que tocas no los conozco
Lo de la potencia de un punto respecto de una circunferencia y su valor único es una consecuencia de se mejanza de triángulos, lo que pasa es que es un poco pesado de explicar y graficar sobre todo. Mejor te dejo el artículo de la Wikipedia donde está explicado.
https://es.wikipedia.org/wiki/Potencia_de_un_punto
Con ello ya queda explicado no solo este ejercicio sino que puede servirte para muchas más cosas.
Lo siento, ya había cerrado el programa de la imagen, te explico sobre la misma que tienes
El ángulo semiinscrito CGE es la mitad del arco CG
El ángulo inscrito GDE = GDC también es la mitad del arco CG
Luego los triángulos CGE y GDE tienen en común el ángulo en E y el ángulo en G del primero es congruente con el ángulo en D del segundo. Al tener dos ángulos con los mismos grados el tercero también lo es y son tríangulos semejantes. Por lo tanto los lados presentan estas relaciones.
$$\begin{align}&\frac{\overline{CG}}{\overline{GD}}=\frac{\overline{GE}}{\overline{DE}}=\frac{\overline{CE}}{\overline{GE}}\\&\\&\text{de la segunda igualdad se deduce}\\&\overline{ED}·\overline{E}C = \overline{EG}^2\\&\\&\text{Haciendo lo mismo en la otra circunferencia llegas a que}\\&\text{los triángulos CHE y HDE son semejantes}\\&\\&\frac{\overline{CH}}{\overline{HD}}=\frac{\overline{HE}}{\overline{DE}}=\frac{\overline{CE}}{\overline{HE}}\\&\\&\overline{ED}·\overline{E}C = \overline{EH}^2\\&\\&\text{igualando}\\&\\&\overline{EG}^2= \overline{EH}^2\\&\\&\overline{EG}= \overline{EH}\\&\\&\end{align}$$Y eso es todo.
