Se pretende fabricar una lata de refresco cilíndrica (con tapa) de 750 cm3 de capacidad.
¿Cuáles deben ser sus
dimensiones (radio “r” y altura “h”) para que se utilice el mínimo de metal
posible (área mínima del material)? Realice
la función del área de la lata así como la gráfica de dicha función, indicando el
valor mínimo del material a emplear.
Respuesta de Valero Angel Serrano Mercadal
1
·
·
¡Hola Lindermann!
La lata tendrá dos dimensiones fundamentales, el radio del cilindro y la altura.
El área será el área lateral más dos veces el área de la base
A =2pi·r·h + 2pi·r^2= 2pi·r(h+r)
Dado que la lata debe tener un volumen determinado se puede hallar la relación entre radio y altura
pi·r^2·h = 750
h = 750 / (pi·r^2)
Con lo cual la función del área tendra una sola variable y será
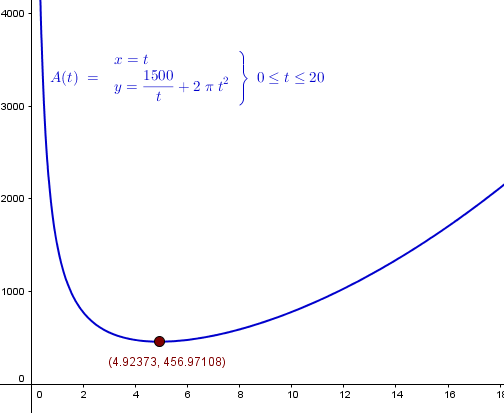
$$\begin{align}&A(r)=2\pi r\left(\frac{750}{\pi r^2}+r \right)=\frac{1500}{r}+2\pi r^2\\&\\&\text{derivamos e igualamos a 0}\\&\\&A'(r)=-\frac{1500}{r^2}+4\pi r=0\\&\\&\text{multiplicamos por r^2}\\&\\&-1500+4\pi r^3=0\\&\\&4\pi r^3=1500\\&\\&r^3= \frac{375}{\pi}\\&\\&r=\sqrt[3]{\frac{375}{\pi}}\approx 4.923725109\,cm\\&\\&h=\frac{750}{\pi \sqrt[3]{\frac{375^2}{\pi^2}}}=\frac{750}{\sqrt[3]{375^2\pi}}=\frac{30}{\sqrt[3]{9\pi}}\approx \\&9.847450218cm\\&\\&\text{El área mínima es}\\&\\&A\left(\sqrt[3]{\frac{375}{\pi}} \right)=\frac{1500}{\sqrt[3]{\frac{375}{\pi}}}+2\pi\left(\sqrt[3]{\frac{375}{\pi}} \right)^2\approx\\&\\&456.9710839cm^2\end{align}$$Y la gráfica es esta:
:
:
