Obtener las raíces del polinomio 𝑃(𝑥)= 𝟒𝒙𝟒+𝟒𝒙𝟑+𝒙𝟐−𝟔𝒙+𝟐
Encontrar las raíces reales y complejas del siguiente polinomio de cuarto grado 𝑃(𝑥)= 𝟒𝒙𝟒+𝟒𝒙𝟑+𝒙𝟐−𝟔𝒙+𝟐
;)
Hola josé Vega!
Sea un polinomio:
$$\begin{align}&Ax^4+Bx^3+Cx^2+Dx+E\end{align}$$por Ruffini primero se buscan las raíces enteras: que son los divisores del término independiente (E): +1,-1,+2,-2 si las prueba veas que ninguna la verifica
Por Ruffini luego pruebo las raíces fraccionarias que son del tipo:
divisores E/divisores A: +1/2 , -1/2 , 1/4 , -1/4 :
1/2 es una raíz doble.
Ahora buscamos las que faltan con el último cociente:
$$\begin{align}&4x^2+8x+8=0\\&simplificando:\\&x^2+2x+2=0\\&\\&x=\frac{-2 \pm \sqrt {4-8}}{2}=\frac{-2 \pm \sqrt {-4}}{2}=\frac{-2 \pm 2i}{2}=\\&\\&-1+i\\&\\&-1-i\end{align}$$saludos
;)
;)
;)
Votar Excelente a todos los expertos te asegura que te sigamos respondiendo
;)
;)
1 respuesta más de otro experto
·
·
¡Hola José!
Por el teorema de la raíz racional. Si existe alguna raíz racional en la ecuación esta será de la forma
p/q
Donde p es un divisor del término constante y q es un divisor del coeficiente de mayor grado.
En esta ecuación
𝟒𝒙^𝟒+𝟒𝒙^𝟑+𝒙^𝟐−𝟔𝒙+𝟐=0
p divide a 2 = {-2, -1, 1, 2}
q divide a 4 = {1,2,4}
Solo tomamos con signo uno de los dos.
Y esto da estas combinaciones posibles
-2, -1, 1, 2, -1/2, 1/2, -1/4, 1/4
Y ahora es cuestión de ir probando. Existen métodos que al probar una descartan otras pero en este caso tan sencillo croe que lo que hacen es complicar más que ayudar.
Vas probando sustituyendo los valores en el polinomio hasta que des con alguno que el valor sea 0. Entonces aplicas Ruffini con ese valor, te queda un polinomio de un grado menor y vuelves a probar con el mismo valor que lo consiguió y con los que quedaban.
Probando con esta vemos que hasta 1/2 no vale 0 el polinomio
P(1/2) = 4/16 + 4/8 + 1/4 -3 + 2 = 1/4 +1/2 + 1/4 - 1 = 1-1=0
Aplicamos Ruffini:
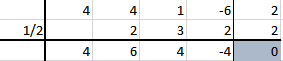
Y ahora continuamos probando con el mismo 1/2 ya que podría ser una raíz doble, trriple, etc.
Sobre si hay que probar evaluando el polinomio o por Ruffini depende de los gustos. A mi me gusta más evaluar el polinomio, eso de ir haciendo pruebas en la caja y borrando porque no te salió no me gusta. Aunque una vez que ya has hecho la caja ya cuesta menos aprovecharla para la continuación. Sea como sea te das cuenta que 1/2 vuelve a servir. Luego aplicando Ruffini dos veces queda:
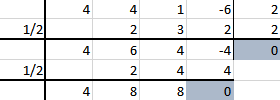
Y esto ya tiene toda la pinta de que no va a tener más soluciones, cuando a y c son positivos es fácil que no las haya.
La ecuación que queda es
4x^2 + 8x + 8 = 0
x^2 + 2x + 2 = 0
$$\begin{align}&x= \frac{-2\pm \sqrt{4-8}}{2}=-1\pm i\\&\\&\text{Luego las raíces son}\\&\\&\left\{\frac 12,\frac 12,-1+i,-1-i \right\}\\&\\&\text{Y la factorizacón es}\\&\\&P(x)=4\left(x-\frac 12 \right)^2(x+1-i)(x+1+i)\end{align}$$No sé si eras tú el que hace unos días preguntabas por el método de Descartes y Ferrari. Olvídate de esas cosas, así como de Cardano, a no ser que las estés estudiando específicamente, son complicadisimas y para eso ya tenemos hoy en día los ordenadores, para que calculen esas respuestas.
Saludos.
:
: