Me podrán apoyar con el siguiente ejercicio les agradezco Amortización3.- Una deuda de $9000.00 se amortiza con abonos semestr
Amortización
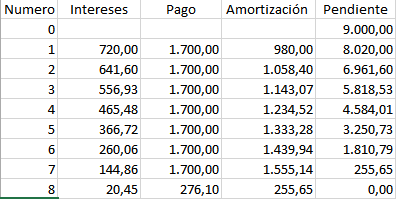
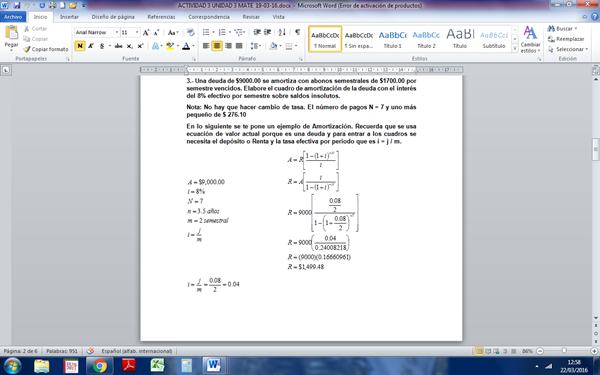
3.- Una deuda de $9000.00 se amortiza con abonos semestrales de $1700.00 por semestre vencidos. Elabore el cuadro de amortización de la deuda con el interés del 8% efectivo por semestre sobre saldos insolutos.
Nota: No hay que hacer cambio de tasa. El número de pagos N = 7 y uno más pequeño de $ 276.10
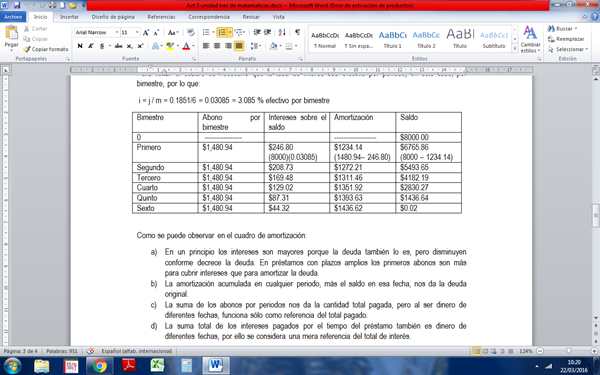
En lo siguiente se te pone un ejemplo de Amortización. Recuerda que se usa ecuación de valor actual porque es una deuda y para entrar a los cuadros se necesita el depósito o Renta y la tasa efectiva por periodo que es i = j / m.
1 Respuesta
·
·
¡Hola Melina!
Nos dan la tasa de interés efectiva del periodo entre pagos. Luego esa tasa es la que hay aplicar al capital vivo para saber los intereses que hay que pagar el próximo periodo. De la cuota que se paga se descuentan los intereses y lo que sobra (o falta) se suma con su signo correspondiente al capital vivo del semestre anterior. Al final, cuando la cuota de 1700 sea superior al capital vivo más intereses no se pagan los 1700 sino ese capital vivo e intereses del último semestre.
El cuadro de amortización, salvo que te guste otro orden de las columnas sería este:
Y efectivamente, hay 7 pagos de $1700 y un pago final de 276,10.
Y eso es todo, saludos.
:
:
Hola Docente le agradezco su apoyo, sin embargo me surgen dudas en el ejemplo me pone la docente queda de esta manera entonces como obtuvo usted los valores para poder graficar
le dejo el ejemplo y le agradezco su apoyo disculpe porque fue mi error no ponerlo antes
Para llenar el cuadro es necesario que la tasa de interés sea efectiva por periodo, en este caso, por bimestre, por lo que:
i = j / m = 0.1851/6 = 0.03085 = 3.085 % efectivo por bimestre
Como se puede observar en el cuadro de amortización:
- En un principio los intereses son mayores porque la deuda también lo es, pero disminuyen conforme decrece la deuda. En préstamos con plazos amplios los primeros abonos son más para cubrir intereses que para amortizar la deuda.
- La amortización acumulada en cualquier periodo, más el saldo en esa fecha, nos da la deuda original.
- La suma de los abonos por periodos nos da la cantidad total pagada, pero al ser dinero de diferentes fechas, funciona sólo como referencia del total pagado.
- La suma total de los intereses pagados por el tiempo del préstamo también es dinero de diferentes fechas, por ello se considera una mera referencia del total de interés.
Perdón Experto por tanta duda pero quedaría la ecuación de esta forma, así obtuvo los datos para hacer la tabla de amortización ? o como se hace le agradezco
No entiendo lo que quieres decir. El cuadro está bien hecho porque salen los 7 pagos y el de 276.10 tal como dice en la respuesta.
El interés no hay ue tocarlo, nos dicen que el 8% efectivo por semestre, y como los pagos son semestrales ese es el interés que debemos usar.
Luego lo único que veo es que la tabla de ellos tiene intercambiadas las columnas segunda y tercera respecto de la mía pero esos da lo mismo y puedes cambiar las de la mía.
Y la tabla de amortización es bien sencilla.
Tomo el pendiente de la fila anterior y lo multiplico por la tasa de nterés
9000 · 0.08 = $720
Esos son los intereses que debo pagar.
De la couta semetral fija resto esos intereses
1700 - 720 = 980$
Esos $980 son los que destino a amortización del préstamo. Ya que la cantidad que pago se destina primero para pagar los intereses y lo que sobra para amortizar la deuda.
Y en la columna pendiente resto del pendiente de la columna superior la amortización que hago
9000 - 980 = $8020
Y ya he completado el ciclo del primer pago, ahora hago lo mismo para el segundo pago, tercero, etc.
Saludos.
:
:
:
:
