Calcular el área lateral de una pirámide

·

·

¡Hola Emmanuel!

Esta es parecida a una que me has pedido explicaciones hace poco. Consisten en como hallar el lado de un triángulo equilátero conociendo la altura (el apotema del hexágono)

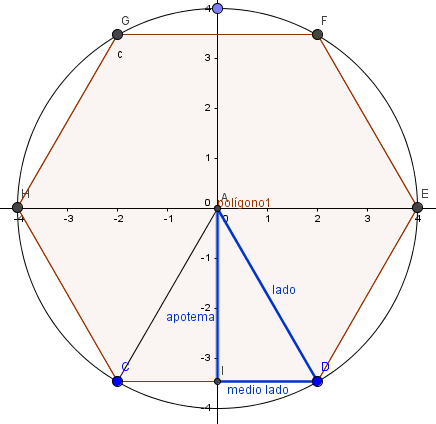
Y de ahí surge esta expresión del teorema de Pitagoras

$$\begin{align}&apotema^2+\left(  \frac {lado}2\right)^2=lado^2\\&\\&apotema^2+ \frac {lado^2}4=lado^2\\&\\&apotema^2 = \frac{3}{4}lado^2\\&\\&lado= \sqrt{\frac {4·apot^2}{3}}=\frac{2 ·apot}{\sqrt 3}=\frac{2·apot· \sqrt 3}{3}\\&\\&Luego\\&\\&lado=\frac{2·8.64· \sqrt 3}{3}= 5.76 \sqrt 3\,cm\\&\\&\text{Ahora necesitamos el apotema de la pirámide}\\&\text{Entre el apotema de l abase, el de la pirámide y}\\&\text{la altura se forma un triángulo rectángulo, de modo que}\\&\\&a_p^2=a_b^2+h^2\\&\\&a_p= \sqrt{a_b^2+h^2}=\sqrt{8.64^2+15^2}=17.31039cm\\&\\&\text{Y el área lateral son 6 triángulos de base el lado}\\&\text{y altura el apotema de la pirámide}\\&\\&A_l=6·\left(\frac{5.76·\sqrt 3·17.31039}{2}  \right)\approx518.09717cm^2\\&\end{align}$$

Y eso es todo, saludos.

:

: