Solución de ejercicios de limites y continuidad:
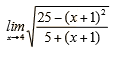
Requiero ayuda con este ejercicio de limites y continuidad.
3 Respuestas
Pues salvo que hay un error, no hay ningún problema y lo puedes calcular directamente evaluando la función en el punto
$$\begin{align}&\lim_{x \to 4} \sqrt{\frac{25-(x+1)^2}{5+(x+1)}}=\sqrt{\frac{25-(4+1)^2}{5+(4+1)}}=\frac{0}{\sqrt{10}}=0\end{align}$$
;)
Hola Panchita!
Evaluemos el límite para ver si da alguna indeterminación:
$$\begin{align}&\lim_{x \to 4} \sqrt{\frac{25-(4+1)^2}{5+(4+1)}}=\sqrt {\frac{0}{10}}=0\end{align}$$luego es directo.
Otra cosa sería si en el denominador pusiera 5-(x+1)=5-(4+1)=0
Ya que tendríamos la indeterminación 0/0 ; pero no es el caso
;)
Abajo tienes la valoración Excelente, puedes cambiarla y aseguratte nuevas respuestas de los expertos
·
·
¡Hola Panchita!
Primero se hace siempre la evaluación de la función.
$$\begin{align}&\lim_{x\to 4} \sqrt{\frac{25-(x+1)^2}{5+(x+1)}}= \sqrt{\frac{25-5^2}{5+5}}=\sqrt{\frac 0{10}}=0\end{align}$$Pues el límite es 0, ya está. Algunas veces ponen algún ejercicio así para ver si el alumno está atento y no le da por hacer cosas raras. Otra posibilidad es que se hayan confundido. Si en el denominador hubieran puesto 5-(x+1) tendríamos la indeterminación 0/0 y habría que hacer más operaciones.
Y eso es todo, espero que te sirva y lo hayas entendido. Aquí estamos los tres principales que te van a resolver algún ejercicio de buena forma en esta página. Debes puntuar excelente a los tres para seguir contando con nosotros.
Saludos.
:
: