Problemas con valor inicial de ecuaciones diferenciales mediante transformada de laplace
Actividad consiste en resolver los problemas con valor inicial de ecuaciones diferenciales mediante el método de transformadas de Laplace:
1 Respuesta
Respuesta de Valero Angel Serrano Mercadal
1
·
·
¡Hola Mauricio!
Estos problemas llevan mucho trabajo, yo no puedo hacerlos todos completos y con todas las explicaciones. Te lo dejo planteado e intenta terminarlo tú.
$$\begin{align}&s^2\mathcal L\{y\}-s+4s\mathcal L\{y\}-4-5\mathcal L\{y\}=\frac{1}{(s-1)^2}\\&\\&(s^2+4s-5)\mathcal L\{y\}=\frac{1}{(s-1)^2}+s+4\\&\\&(s^2+4s-5)\mathcal L\{y\}=\frac{1+s(s-1)^2+4(s-1)^2}{(s-1)^2}\\&\\&\mathcal L\{y\}=\frac{1+s(s-1)^2+4(s-1)^2}{(s-1)^2(s^2+4s-5)}\\&\\&\mathcal L\{y\}=\frac{1+s(s-1)^2+4(s-1)^2}{(s-1)^2(s-1)(s+5)}\\&\\&\mathcal L\{y\}=\frac{1+s(s-1)^2+4(s-1)^2}{(s-1)^3(s+5)}\\&\\&\text{Y las fracciones simples son}\\&\\&\mathcal L\{y\}=\frac{a}{s-1}+\frac{b}{(s-1)^2}+\frac{c}{(s-1)^3}+\frac{d}{s+5}\\&\\&\text{Y lo dejo, mucha suerte porque no será nada fácil}\end{align}$$Te dejo la solución que debe dar, aunque no me gusta la forma como la han dejado.
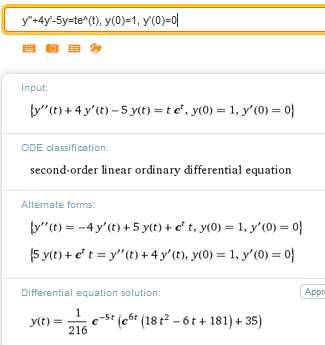
Y eso es todo, saludos. Si no te sale dímelo pero tendrás que mandar lo que hayas hecho.
Saludos.
:
:
