Demostracion de variable compleja2...semicirculo!
Por un error de planteamiento vuelvo a poner la pregunta espero me apoyen... Aclarando que solo es el referente al semicírculo, de antemano muchas gracias!
- Sea C_1 es el semicírculo que va de -1 a 1 . Como se muestra en la figura.
Demostrar que:
∫_(C_1)〖z ̅dz=-πi 〗
Donde z ̅ es el conjugado de z.
1 Respuesta
Respuesta de Valero Angel Serrano Mercadal
1
·
·
¡Hola Zankass!
Eso suponía, pero como este tema lo llevo prendido con alfileres prefiero hacer las cuentas sobre seguro.
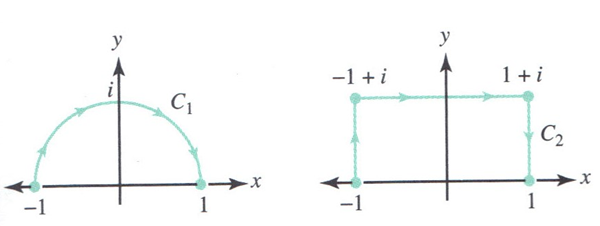
Lo único que hay que hacer es parametrizar el semícirculo de modo que tenga ese origen, ese sentido y ese final.
$$\begin{align}&\text{el semi círculo de radio 1centrado en el origen con }\\&\text{sentido positivo tiene ecuación }\\&\gamma(t)=e^{it}\quad con \; 0\le t \le \pi\\&\text{ya que eso es}\\&\gamma(t)= cost+i·sent\\&\text{y se recorre en contrario a las agujas del reloj.}\\&\text{El recorrido que queremos nosotros será esa}\\&\text{misma función pero entre }\pi\; y\; 0\\&\\&\text{La función }es\\&f(z)=\overline z\\&f(\gamma(t))=\overline{\gamma(t)}= \overline {cost+i sent}=\\& cost-i·sent=e^{-it}\\&\\&\text{Y la derivada del camino es}\\&\gamma'(t)=ie^{it}\\&\\&\text{Luego la integral por definición es}\\&\\&\int_{C_1} \overline z\, dz =\int_{\pi}^0 \overline {\gamma(t)}·\gamma'(t)\;dt =\\&\\&\int_{\pi}^0(e^{-it}·i·e^{it})dt=\int_{\pi}^0i\,dt=i·\bigg|_{\pi}^0=\\&\\&i·(0-\pi)=-\pi i\end{align}$$Y eso es todo saludos.
·
·
