Buen día un cordial saludo, algunos de ustedes me podría colaborar, con la explicación de estas integrales :
Tengo muchas dificultades con estas integrales, alguien me podría explicar alguna de estas, seria de gran ayuda entender un poco más ... Les agradezco
2 respuestas
;)
Hola alfonso!
El 7 y 8 se hacen con sustituciones directas:
7.-
Como ya te expliqué en la anterior pregunta, observa en el integrando( función a integrar)
Que tienes una parte multiplicando al dx, que es el senx, que es la derivada de otra parte (cosx), pues la sustitución es cosx=t
$$\begin{align}&\int_0^{\frac{\pi}{2}} \frac{senx}{25+\cos^2x}dx=\\&\\&cosx=t\\&-senxdx=dt\\&\\&x=0 \rightarrow t=cos0=1\\&x=\frac{\pi}{2} \rightarrow t=\cos \frac{ \pi}{2}=0\\&\\&== \int_1^0 \frac{1}{25 +t^2}(-dt)=- \int_1^0 \frac{1}{\frac{25}{25}(25 +t^2)} dt=- \frac{1}{25} \int \frac{1}{\frac{25 +t^2}{25}}dt=\\&\\&-\frac{1}{25} \int_1^0 \frac{1}{1 +(\frac{t}{5})^2}dt= -\frac{1}{25} \Bigg [arctan( \frac{t}{5})·5 \Bigg]_1^0=\frac{-1}{5} \Big(arctan0-arctan \frac{t}{5})= \frac{1}{5}arctan(\frac{t}{5})+C\end{align}$$;)
8.-
$$\begin{align}&e^{4x}=t\\&\\&e^{4x}·4dx=dt\\&e^{4x}dx= \frac{dt}{4}\\&\\&\int \frac{\frac{dt}{4}}{\sqrt{4-t^2}}=\frac{1}{4} \int \frac{dt}{ \sqrt {(4-t^2)·\frac{4}{4}}}= \frac{1}{4}·\frac{1}{2} \int \frac{dt}{\sqrt{\frac{4-t^2}{4}}}=\\&\\&=\frac{1}{8} \int \frac{dt}{ \sqrt {1-(\frac{t}{2})^2}}=\frac{1}{8} arcsen (\frac{t}{2})·2=\frac{1}{4} arcsen( \frac {e^{4x}}{2})+C\end{align}$$;)
;)
;)
en el 7 la solución es 1/5 arctan(1/5)
Dejé la t, donde tenia que escribir 1
;);)
;)
·
·
¡Hola Alfonso!
Estas integrales deben mandarse de una en una. El 6 es complicadísimo y lo haré con cambios hipérbolicos, con trigonométricos que la haga el profesor si quiere.
$$\begin{align}&\int_{0}^1 \frac{\sqrt x}{\sqrt{x+1}}dx\\&\\&x=sh^2t\\&dx= 2sh\,t·ch\,t\;dt\\&x=0\implies t=argsh(0)= ln(0+\sqrt{1+0^2})=0\\&x=1\implies t=argsh(1) = ln(1+\sqrt{1^2+1})=ln(1+ \sqrt 2)\\&\\&\text{Ojo, vamos a cambiar los extremos de integración}\\&\text{no hará falta deshacer el cambio para evaluarla}\\&\\&=\int_0^{ln(1+ \sqrt 2)}\frac {sh\,t}{\sqrt{1+sh^2t}}·2sh\,t·ch\,t\;dt=\\&\\&\text{Como }1+sh^2t= ch^2t\\&\\&=\int_0^{ln(1+ \sqrt 2)}\frac {sh\,t}{ch\,t}·2sh\,t·ch\,t\;dt=\\&\\&=2\int _0^{ln(1+ \sqrt 2)}sh^2t\;dt=\\&\\&\text{En la página no te lo pone pero de}\\&ch\,2t=ch^2t+sh^2t\\&-1+ch\,2t=ch^2t-1+sh^2t=sh^2t+sh^2t=2sh^2t\implies\\&\\&sh^2t=\frac{-1+ch\,2t}{2}\\&\\&=2\int_0^{ln(1+ \sqrt 2)}\left(\frac{-1+ch\,2t}{2}\right)\;dt=\\&\\&2\left[-\frac t2 + \frac{sh\, 2t}{4} \right]_0^{ln(1+ \sqrt 2)}=\\&\\&\left[ -t + \frac{sh\, 2t}{2} \right]_0^{ln(1+ \sqrt 2)}=-ln(1+\sqrt 2)+\frac{sh(2ln(1+\sqrt 2)}{2}-0-\frac{sh\,0}{2}=\\&\\&-ln(1+\sqrt 2)+\frac{sh(ln[(1+\sqrt 2)^2]}{2}-0-0=\\&\\&-ln(1+\sqrt 2)+\frac{e^{ln[(1+\sqrt 2)^2]}-e^{-ln[(1+\sqrt 2)^2]}}{4}=\\&\\&-ln(1+\sqrt 2)+\frac{(1+ \sqrt 2)^2-(1+\sqrt 2)^{-2}}{4}\approx\\&\\&0.53283997535355\end{align}$$Y lo que hace falta es comprobar si está bien, para ello echamos mano de la famosa página de Wolfram Alpha
http://www.wolframalpha.com/input/?i=int+sqrt%28x%29%2Fsqrt%28x%2B1%29+form+0+to+1
Que es muy probable que n se pueda pinchar y tengas que copiar y pegar en el navegador, o si no aquí tienes o que sale
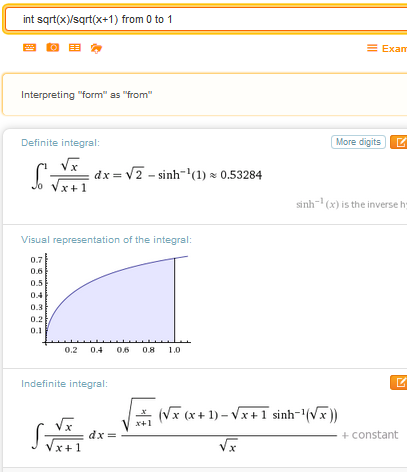
Que como ves es lo mismo. De todas formas me gusta más la expresión real de la respuesta que da Wolfram Alpha que la mía
Voy a ver como habría quedado la mía si no hubieramos hecho cambio de extremos, entonces es la integral entre 0 y 1 y hay que deshacer el cambio
$$\begin{align}& -t + \frac{sh\, 2t}{2} =\\&\\&como \\&x=sh^2t\implies{}t=argsh \sqrt x\\&sh2t=2\,sh\,t·ch\,t\\&\\&=-argsh\,\sqrt x+sht·cht=\\&\\&-argsh \sqrt x+\sqrt x·\sqrt{1+sh^2t}=\\&\\&-argsh \sqrt x+\sqrt x \sqrt{1+x}\\&\\&\text{que evaluado entre 0 y 1 es}\\&\\&\left[\sqrt x \sqrt{1+x}-argsh \sqrt x\right]_0^1=\sqrt 2-argsh\,1\end{align}$$Pues sí sale esa misma respuesta. A veces si no deshaces los cambios queda una expresión peor de la respuesta, aunque sea el mismo valor. Luego lo que puedes hacer es hacer primero la integral indefinida sin extremos de integración y tras deshacer el cambio la evalúas entre 0 y 1 tal como he deshecho y evaluado ahora mismo.
Y esto es todo, para mi es es mucho más sencillo. Pero si no conoces estas funciones te resultará mucho más complicado. Te remito al artículo de la Wikipedia sobre funciones hiperbólicas por si no las conoces.
Y esto ha sido todo, ojala lo hayas entendido.
Saludos.
:
: