Muy buenas, se me presentan estos dos problemas de calculo, les pido colaboracion
- Hallar el volumen generado por la rotación del área del primer cuadrante limitada por la parábola y=8x y la ordenada correspondiente a x=2 con respeto al eje x, como lo muestra la figura.
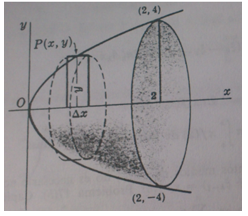
La región limitada por la gráfica se gira alrededor del eje x. Hallar el área de la superficie lateral del solido resultante.
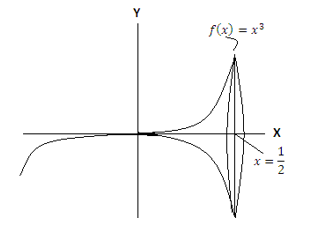
2 Respuestas
Respuesta de Lucas m
1
;)
Hola joan!
1.-
$$\begin{align}&V=\pi \int_0^2 f(x)^2dx=\pi \int_0^2(8x)^2dx=64 \pi \frac{x^3 }{3} \Bigg |_0^2=64 \pi \frac{8}{3}=4096 \frac{ \pi}{3}\end{align}$$saludos
;)
;)
muchas gracias por su colaboración, me genera una duda respetado lucas m, en el ultimo paso donde tenemos 64π(8/3)=4096π/3, la respuesta que me da es 64π(8/3)=512π/3, agradezco si me puede aclarar esa duda.
2.-)
$$\begin{align}&A_l=2 \pi \int_a^b f(x)\sqrt{1+[f'(x)]^2}dx=\\&\\&2 \pi \int_0^\frac{1}{2} x^3 \sqrt{1+(3x^2)^2}dx=\\&\\&2 \pi \int_0^\frac{1}{2} x^3 \sqrt{1+9x^4}dx=\\&1+9x^4=t\\&36x^3dx=dt\\&x=0 \Rightarrow t=1\\&x=\frac{1}{2} \rightarrow t=1+9 \frac{1}{16}=\frac{25}{16}\\&\\&2 \pi \int_1^\frac{25}{16} t^\frac{1}{2} \frac{dt}{36}= \frac{2 \pi}{36} t^\frac{3}{2} \frac{2}{3}=\frac{4 \pi}{108} t^\frac{3}{2} \Bigg|_1^{\frac{25}{16}}=\\&\\&\frac{4 \pi} {108}\Bigg[\Big(\frac{25}{16}\Big)^{\frac{3}{2}}-1 \Bigg ]=\frac{4 \pi} {108} \Big(\frac{125}{64}-1 \Big)=\frac{61 \pi}{1728} u^2\end{align}$$;)
;)
;)
Tienes razón, copié mal el número, es 512
;)
Respuesta de Valero Angel Serrano Mercadal
1
·
·
¡Hola Joan!
En el primer ejercicio dices la parábola y = 8x, pero eso no es una parábola, revisa el enunciado.
¡Jope, el 2 es el complicado de verdad!
$$\begin{align}&S= 2\pi\int_{x_1}^{x_2}f(x) \sqrt{1+(f'(x))^2}dx\\&\\&f(x) = x^3\\&f'(x)=3x^2\\&x_1=0\\&x_2=\frac 12\\&\\&S=2\pi\int_0^{\frac 12} 3x \sqrt{1+9x^4} dx\\&\\&\text{De momento me conformo con esta indefinida}\\&\\&I=\int 3x \sqrt{1+9x^4} dx\\&\\&3x^2=sh\,u\\&6x\;dx= ch\,u\; du\implies 3x\;dx= \frac 12 ch\,u\;du\\&donde\\&sh\,u= \text{seno hiperbólico de u}\\&ch\,u=\text{coseno hiperbólico de u}\\&\\&I=\frac 12\int ch\,u \sqrt{1+sh^2 u}\;du=\\&\\&\frac 12 \int ch\,u·\sqrt{ch^2\,u} du= \frac 12\int ch^2 u\;du=\\&\\&\frac 12\int\left(\frac 12+\frac{ch\,2u}{2} \right)du= \frac u4+\frac{sh\;2u}{8}+C=\\&\\&\frac u4+\frac{2sh\,u·ch\,u}{8}+C=\\&\\&\frac{arg\,sh(3x^2)}4+\frac{3x^2 \sqrt{1+9x^4}}{4}+C =\\&\\&\frac{ln(3x^2+\sqrt{1+9x^4})+3x^2 \sqrt{1+9x^4}}{4}+C\\&\\&\text{Luego la superficie es}\\&\\&S=2\pi·\frac{ln(3x^2+\sqrt{1+9x^4})+3x^2 \sqrt{1+9x^4}}{4}\bigg|_0^{\frac 12}\\&\\&\frac \pi 2 \left(ln\left( \frac 34+\sqrt {1+\frac{9}{16}} \right) +\frac 34 \sqrt {1+\frac{9}{16}} -ln\,1-0\right)=\\&\\&\frac{\pi}{2}\left(ln\left( \frac 34+\frac 54\right)+\frac 34·\frac 54\right)=\\&\\&\frac{\pi}{2}\left(ln\,2+\frac {15}{16}\right)\approx 2.561414602\end{align}$$Repásalo todo porque lo he hecho con prisas que tengo que irme.
Saludos.
:
: