·
·
¡Hola Llaq!
Este Jorge Herrera no se cansa de pegar enlaces al tuntún que no resuelven el problema y hacen perder tiempo. ¡Vaya experto! No sé como no se da cuenta que manifiesta más ignorancia en matemáticas que un chaval de 14 años.
Si tu consideras el segmento entre los puntos P1 y P2 y añades las proyecciones horizontal y vertical tendrás un triángulo rectángulo.
Si consideras el segmento entre P1 y PP y añades las proyecciones tendrás otro triángulo rectángulo semejante al primero, ya que tienen en común el ángulo en P1, y todos los lados son paralelos.
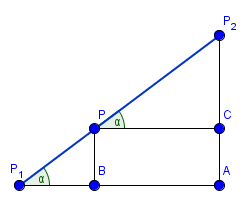
Por ser semejantes los triángulos
$$\begin{align}&P_1PB \quad y\quad P_1P_2A \\&\\&\text{se cumplen estas relaciones.}\\&\\&\frac{\overline{P_1P}}{\overline{P_1P_2}}=\frac{\overline{P_1B}}{\overline{P_1A}}=\frac{\overline{BP}}{\overline{AP_2}}\\&\\&r=\frac{r_1}{r_2}=\frac{\overline{P_1B}}{\overline{P_1A}}=\frac{\overline{BP}}{\overline{AP_2}}\\&\\&\overline{P_1B}=r·\overline{P_1A}\\&\\&\overline{BP}=r·\overline{AP_2}\\&\\&\text{P es la sumas de un punto y un vector}\\&\\&P(x,y)=(x_1,y_1)+\vec{P_1P}=\\&\\&(x_1+\overline{P_1B},\;y_1+\overline {PB})=\\&\\&(x_1+r·\overline{P_1A}, \;y_1+r·\overline{AP_2})=\\&\\&(x_1+r(x_2-x_1), \;y_1+r(y_2-y_1))=\\&\\&\left(x_1+\frac {r_1}{r_2}(x_2-x_1), \;y_1+\frac{r_1}{r_2}(y_2-y_1)\right)=\\&\\&\left(\frac{r_2x_1+r_1x_2-r_1x_1}{r_2}, \;\frac{r_2y_1+r_1y_2-r_1y_1}{r_2})\right)=\\&\\&\left(\frac{(r_2-r_1)x_1+r_1x_2}{r_2}, \;\frac{(r_2-r_1)y_1+r_1y_2}{r_2}\right)\\&\\&\text{que separando las componentes es}\\&\\&x=\frac{(r_2-r_1)x_1+r_1x_2}{r_2}\\&\\&y=\frac{(r_2-r_1)y_1+r_1y_2}{r_2}\\&\\&\text{Se te olvidó un subíndice en las fórmulas,}\\&\text{o escribirlas así para que estén bien}\\&\\&x=\frac{(r_2-r_1)x_1}{r_2}+rx_2\\&\\&y=\frac{(r_2-r_1)y_1}{r_2}+ry_2\\&\\&\text{aunque la forma más concisa es}\\&\\&x=x_1+r(x_2-x_1)\\&\\&y=y_1+r(y_2-y_1)\\&\\&\end{align}$$Y eso es todo, salu_dos.
·
·

