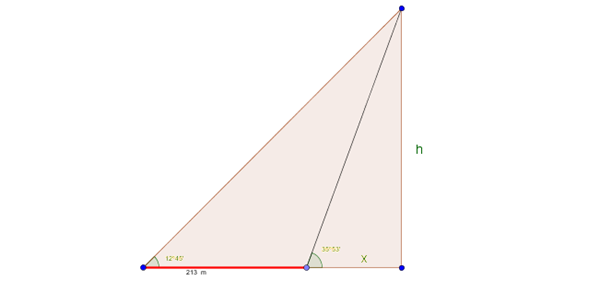
¿Cuál es la altura de la colina?
El punto más alto de una colina se observa con un angulo de elevación de 12°45'. Al acercarse a la colina 213 m, el punto más alto se observa con un angulo de elevación de 35°53'. ¿Cuál es la altura de la colina?
2 respuestas
Respuesta de Lucas m
1
Respuesta de Valero Angel Serrano Mercadal