Eecuaciones de grado n mediante el método correcto para resolver las ecuaciones
Tengo la siguiente ecuacion diferencial
$$\begin{align}&x^3y''' - 3x^2y'' +2xy' - y = 0\end{align}$$lo intente haciendo
y=x^m
y'=mx^(m-1)
Hasta y'''
Y luego sustituyo en la ecuacion diferencial, ¿no se si es correcto o como debo atacar esta ecuacion?
1 Respuesta
·
·
¡Hola Omar!
Si, ese es méodo correcto, ya que todos los términos de la ecuación se transforman en monomios del mismo grado y se puede despejar m. Solo que esta vez te quedara una ecuación de grado 3, ya deremos si se puede resolver fácilmente
$$\begin{align}&y=x^m\\&y'=mx^{m-1}\\&y''=m(m-1)x^{m-2}\\&y'''=m(m-1)(m-2)x^{m-3}\\&\\&x^3·m(m-1)(m-2)x^{m-3}-3x^2·m(m-1)x^{m-2}+2x·mx^{m-1}-x^m=0\\&\\&m(m-1)(m-2)x^m-3m(m-1)x^m+2mx^m-x^m=0\\&\\&\text{La solución }y=x^m=0\\&\text{siempre está, pero no es la que nos interesa, luego}\\&\text{dividimos por }x^m\\&\\&m(m-1)(m-2)-3m(m-1)+2m-1=0\\&m^3-2m^2-m^2+2m-3m^2+3m+2m-1=0\\&m^3-6m^2+7m-1=0\\&\\&\text{Y esto solo puede tener soluciones racionales 1 o -1}\\&\\&Para\; m=1\\&1-6+7-1=1\\&\\&Para\;m -1\\&-1-6-7-1=0\end{align}$$Luego la única respuesa asequible es
y=0
Las otras las buscaremos con WolframAlpha por ejemplo:
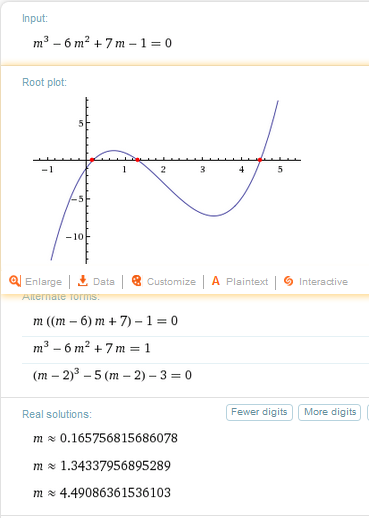
Esos son los exponentes de
y=x^m
Que son solución de la ecuación diferencial. Yo no sé que hacéis cuando llega un problema de estos, sería un abuso pretender que lo solucionaráis con métodos como el de Newton-Rapson por ejemplo, luego deberían tener más cuidado al elegirlos.
Y eso es todo, salu_dos.
:
:
Bien es cierto que la ecuación de tercer grado tiene una fórmula. Aun no he conseguido terminar de resolver ninguna en mi vida a través de esa fórmula.
