Dominio y simetría de una función

·

·

¡Hola Elsepu!

Es un cociente de polinomios que estaán definidos en todo R. EL cociente también lo estará salvo en los puntos donde el denominador valga 0. Y desde aquí ya veo que no hay puntos donde valga 0 ya que el discriminante de la ecuación

b^2 - 4ac = 36 - 40 = -4 

Es negativo y por lo tanto la ecuación no tiene soluciones reales.

Luego el dominio es todo R.

Y las simetrías en los polinomios se dan en dos casos:

1) Cuando todas las potencias son pares se produce

p(x) = p(-x)

Y hay simetría respecto del eje Y

2) Cuando todas las potencias son impares se produce

p(x) = -p(-x)

Y hay simetría central respecto el punto (0,0)

Aquí no se da ninguna de esas dos simetrías ya que hay dos términos con exponente par y otro impar.

Pero al ser el numerador una constante, hay una simetría respecto al eje que pasa por el vértice de la parábola del denominador, que es el punto:

v= -b/2a = 6/2 = 3

Luego hay simetría respecto de la recta x=3

Véase aquí:

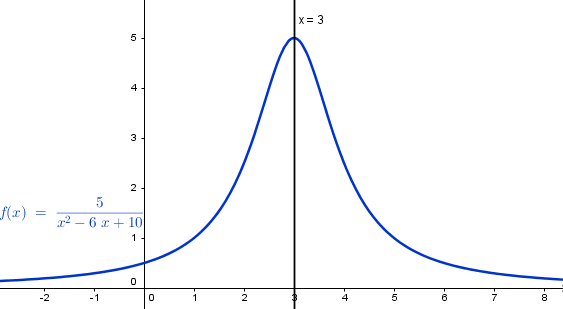
Y eso es todo, salu_dos.

:

: