La función de densidad de las mediciones codificadas...
1) El tiempo que pasa, en horas, para que un radar detecte entre conductores sucesivos a los que exceden los límites de velocidad es una variable aleatoria continua con una función de distribución acumulativa:
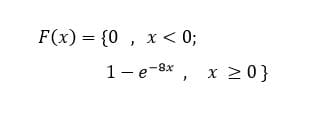
Calcule la probabilidad de que el tiempo que pase para que el radar detecte entre conductores sucesivos a los que exceden los límites de velocidad sea menor de 12 minutos.
* Usando la función de densidad de probabilidad de x.
2)La función de densidad de las mediciones codificadas del diámetro de paso de los hilos de un encaje es:
$$\begin{align}&f(x)= 4 / [3,1416 (1+x^2)] \end{align}$$
* Calcular el valor esperado de x.
Me pueden explicar
1 respuesta
·
·
¡Hola Lecarpio!
Una vez tenemos la función la función de distribución, la probabilidad se calcula así:
P(a<= X <= b) = F(b) - F(a)
P(0 <= X <= 12) = F(12) - F(0) =
Ojo, la función de distribución mide el tiempo en horas, luego
12m = 12/60 h = 1/5 h = 0.2h
P(0 <= X <= 0.2) = F(0.2) - F(0) =
1 - e^(-8·0.2) - [1 - e^(-8·0)] = 1 - e^(-1.6) - (1-1) = 1 - e^(-1.6) = 0.798103482
-------------------------
El valor esparado de una variable aleatoria conocida su función de densidad x es:
$$\begin{align}&E(X)=\int_{-\infty}^{\infty}x·f(x)\;dx\\&\\&\text{En nuestro caso f(x)=0 fuera de (0, 1) luego}\\&\\&E(X)=\int_0^1 x·\frac{4}{\pi(1+x^2)}dx=\frac 2\pi\int \frac{2x}{1+x^2}dx=\\&\\&\frac 2\pi ln(1+x^2)\bigg|_0^1= \frac 2\pi\left(ln2-ln1 \right)=\frac{2\,ln2}{\pi}=\frac{ln \,4}{\pi}\approx 0.4412712\end{align}$$Y eso es todo.
S a l u d o s.
:
:
