¿Cuál es el área de la región limitada?

·

·

¡Hola Milena!

Pues hacemos la gráfica, yo prefiero resolverlos sin gráfica, pero como lo piden.

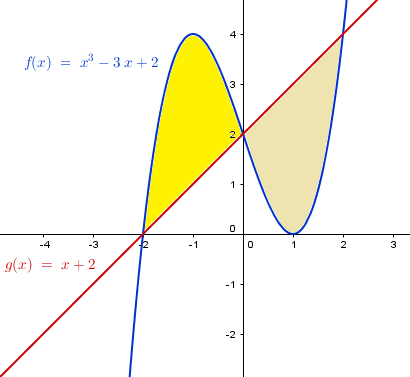
Vemos que son dos partes con simetría central en (0,2) pero como eso no es una cosa corriente ni que se vea inmediatamente a la vista de las ecuaciones vamos a ignorarlo.

Lo que si vamos a calcular aunque se vea son los puntos de intersección

x^3 - 3x + 2 = x+2

x^3-4x=0

x(x^2-4) = 0

x(x+2)(x-2) =0

Luego se cortan en 0, -2 y 2, hay que hacer dos integrales de la función diferencia que es

x^3 - 4x

Ahora si que nos damos cuenta que esa función es impar, luego el modulo de la integral en [-2, 0]  es el mismo que el de la integral en [0,2].  Asi que finalmente integraremos solo en [0,2] y multiplicamos por 2.

$$\begin{align}&A=2\left|\int_0^2 (x^3-4x)dx\right|=\\&\\&2\left|\left[\frac{x^4}{4}-2x^2  \right]_0^2\right|=2·|4-8|=2·4=8\end{align}$$

Y eso es todo,   s a l u d o s.

:

: