Coordenadas en el plano cartesiano
Es una pregunta de Geometría analítica, la cual se detalla en las siguientes imágenes.
1 respuesta
·
·
¡Hola Francisco!
1)
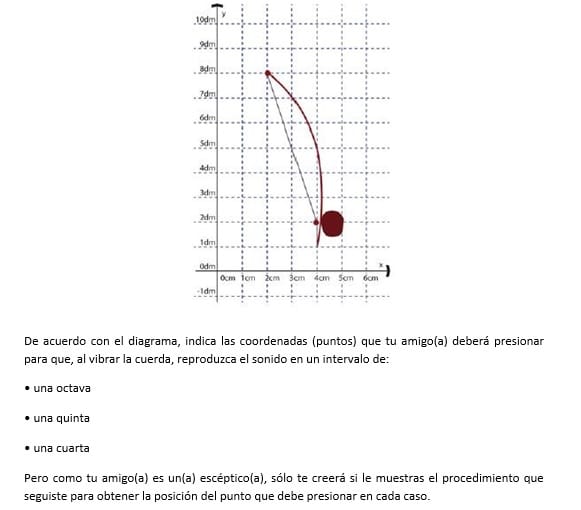
El punto superior del segmento es A(2cm, 8dm)
El punto inferior es B(4cm, 1dm)
·
2)
Para una octava se debe tomar 1/2 del segmento como cuerda vibrante
Para una quinta debe tomar 2/3 del segmento
Para una cuarta se debe tomar 3/4 del segmento
·
3)
Suponemos que la parte donde se toca y vibra es la superior del segmento, la que empieza en A
El segmento en X mide: 4cm-2x=2cm
y en Y mide: 8dm-1dm=7dm
Para una octava tomaremos:
en X, 1/2 de 2cm = 1cm
en Y, 1/2 de 7dm = 7/2dm
Esto se debe añadir como un vector al punto A para obtener el punto de pulsación, en X sumando, pero en Y restando
(2cm, 8dm) + (1cm, -7/2dm) = (3cm, 9/2dm)
·
Para una quinta sera lo mismo con 2/3 de 2cm y 7dm
(2cm, 8dm) + (4/3cm, - 14/3dm) = (10/3cm, 10/3dm)
·
Para una cuarta será lo mismo con 3/4 de 2cm y 7dm.
(2cm, 8dm) + (6/4cm, - 21/4dm) = (7/2cm, 11/4dm)
·
4)
Esta es la gráfica:
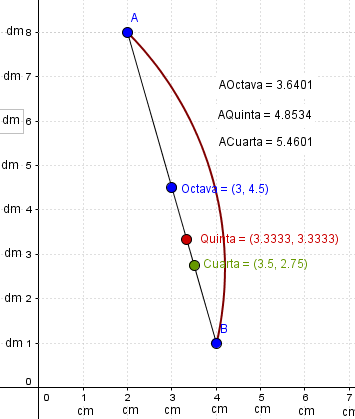
5)
Ya he puesto las longitudes de los segmentos que me ha dado el programa de gráficas, pero ahora las calcularé correctamente por la tontería que han tenido de poner un eje en decímetros y otro en centímetros. Lo pasaremos todo a centímetros.
$$\begin{align}&A=(2cm,8dm) = (2cm,80cm)\\&\\&Octava\left(3cm,\frac 92 dm\right)=(3cm,45cm)\\&\\&Quinta\left(\frac{10}{3}cm,\frac {10}3dm\right)=\left(\frac{10}3cm,\frac {100}{3}cm \right)\\&\\&Cuarta\left(\frac 72cm, \frac{11}4dm \right)=\left(\frac 72 cm,\frac {55}2cm \right)\\&\\&B(4cm,1dm)=(4cm,10cm)\\&\\&\overline{AB}=\sqrt{(4-2)^2+(10-80)^2}=\sqrt{4904}=70.0285656cm\\&\\&\\&\overline{AO_{ctava}}=\sqrt{(3-2)^2+(45-80)^2}= \sqrt{1226}=35.0142828cm\\&\text{es justo la mitad de la longitud del segmento}\\&\\&\\&\overline{AQ_{uinta}}=\sqrt{\left(\frac {10}3-2\right)^2+\left(\frac{100}{3}-80 \right)^2}=\\&\\&\sqrt{ \frac{4^2}{3^2}+\frac{(-140)^2}{3^2}}= \frac{\sqrt{19616}}{3}=46.6857104cm\\&\\&\frac 23 de\; 70.0285656cm=46.6857104cm\\&\text{Está bien}\\&\\&\\&\overline{AC_{uarta}}=\sqrt{\left(\frac 72-2 \right)^2+\left(\frac {55}2-80 \right)^2}=\\&\\&\sqrt{\frac{3^2}{2^2}+\frac{(-105)^2}{2^2}}=\frac{\sqrt{11034}}{2}=52.5214242cm\\&\\&\frac 34 de \;70.0285656cm=52.5214242cm\\&\text{Está bien}\end{align}$$6) Ya se tuvo en cuenta.
Y eso es todo, S a l u d o s.
·
·
