Calcular el Solido de Revolución

·

·

¡Hola Jaime!

Sí, para eso están los cascarones, para calcular el volumen de sólidos girando alrededor del eje Y cuando nos dan la función f(x), sin tener que calcular la función inversa.

Los puntos de corte de f(x) con eje X son

x^3-x= 0

x(x^2-1) = 0

x=0

x^2-1=0

x^2=1

x=-1

x=1

Mejor que haga la gráfica, creo que has pasado algo por alto

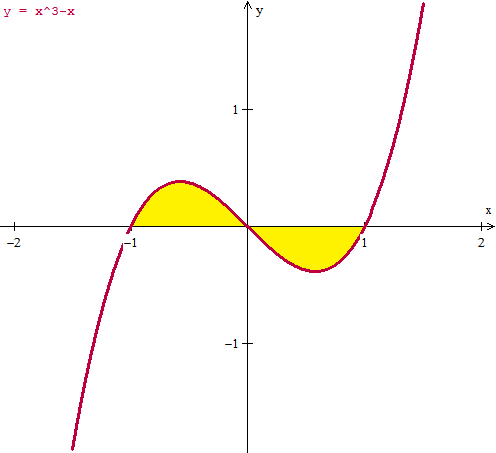
La región que genera volumen no es solo la [0,1], la [-1,0] tambien genera volumen que se suma al anterior.

Por simetría, ya que la función es impar, puedes poner el doble del volumen anterior.

Y si lo quieres hacer sin simetrías debes tener mucho cuidado para que no se compensen volúmenes positivos con negativos, hay que hacer dos integrales y sumar los módulos de cada una. Es lo malo del método de los cascarones, que da volúmenes negativos.

$$\begin{align}&V=2\pi\left|\int_{-1}^0 x(x^3-x)dx\right|+2\pi\left|\int_{0}^1 x(x^3-x)dx\right|=\\&\\&2\pi\left|\left[\frac{x^5}{5}-\frac {x^3}3  \right]_{-1}^0\right|+2\pi\left| \left[\frac{x^5}{5}-\frac {x^3}3  \right]_{0}^1\right|=\\&\\&2\pi\left|\frac 15-\frac 13 \right|+2\pi\left|\frac 15-\frac 13 \right|=2\pi\left|-\frac 2{15}\right|+2\pi\left|-\frac 2{15}\right|=\frac{8\pi}{15}\\&\end{align}$$

Y eso es todo, espero que te sirva.

Sa lu dos.

_

_