Problemas de aplicación de reglas de derivadas!
Por medio de las reglas de la derivación, hallar las siguientes derivadas
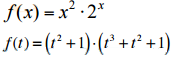
2 Respuestas
U V d/dx(t^2 +1)=2t d/dx(t^3 +t^2 +1)=3t^2+2t
f(t)=(t^2 +1).(t^3 +t^2 +1)
t`=(t^2 +1)d/dx(t^3 +t^2 +1)+(t^3 +t^2 +1)d/dx(t^2 +1)
t`=(t^2 +1) (3t^2 +2t)+(t^3 +t^2 +1) (2t +1)
t`=3t^4 +2t^3 +3t^2 +2t +2t^4 +2t^3 +2t
t`=5t^4 +4t^3 +3t^2 +4t
u v
2.- f(x)= (x^2)(2^x) d/dx a^u=a^u lna d/dx u
f`(x)= (x^2)d/dx(2^x)+(2^x)d/dx(x^2)
f`(x)=(x^2)(2^x ln2)+(2^x)(2x)
f`(x)=2^x ln(2) x^2 + 2x 2^x
simplificado f`(x)=2^(x+1) x + 2^x x^2 ln(2)
·
·
¡Hola Panchita!
Pongo primero las reglas que se necesitarán.
$$\begin{align}&(f+g)'=f'+g'\\&(fg)' = f'g+fg'\\&(x^n)'=nx^{n-1}\\&(a^x)'=a^x·ln\,a\\&\\&1) f(x) = x^2·2x\\&\\&f'(x)=(x^2)'·2^x+x^2·(2^x)'= 2x·2^x+x^2·2^x·ln\,a=\\&\\&\text{sacaremos factor común por decir que hacemos algo}\\&\\&x·2^x·(2+x·ln\,a)\\&\\&\\&4) f(t)=(t^2+1)·(t^3+t^2+1)\\&\\&f'(t)=(t^2+1)'·(t^3+t^2+1)+(t^2+1)·(t^3+t^2+1)'=\\&\\&2t(t^3+t^2+1)+(t^2+1)(3t^2+2t) =\\&\\&2t^4+2t^3+2t+3t^4+2t^3+3t^2+2t=\\&\\&5t^4+4t^3+3t^2+4t\\&\end{align}$$Y eso es todo, s a l u d o s!
:
:
La respuesta está perfecta, tendrías que valorarla con Excelente, si no no contestaré más tus preguntas. Tú tampoco admitirías 1 un punto en una respuesta que vale 2 si la hubieras respondido a la perfección. Puedes cambiar la nota abajo pinchando donde pone votada.
S a l u do s.
_
_
Hola,,,,,siento mi primera nota, lo estaba viendo en el cel y solo me permitió asignar esa nota...y no me dejaba cambiarla....le agradezco mucho toda su colaboración-..¡Gracias!