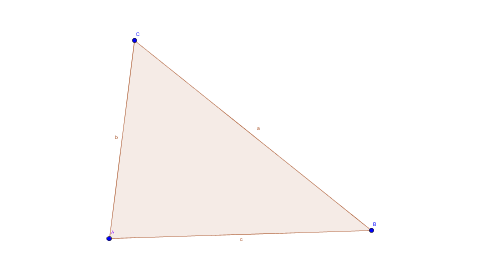
Solucionar el triangulo, con ley de seno
Y cuyas dimensiones son:
c= 12 cm
b= 11 cm
angulo C= 80 °
Por favor con el procedimiento paso a paso
Respuesta de Lucas m
1
;)
Hola Majo!
Ley de los senos:
$$\begin{align}&\frac{a}{senA}=\frac{b}{senB}=\frac{c}{senC}\\&\\&\frac{11}{senB}=\frac{12}{sen80º} \Rightarrow 12 senB=11sen80º \Rightarrow senB=\frac{11}{12}sen80º=0.9027\\&\\&B=arcsen(0.9027)=64º30'55''\\&\\&A=180º-(C+B)=35º29'5''\\&\\&\frac{a}{senA}=\frac{c}{senC}\\&\\&a=c \frac{senA}{senC}=12 \frac{sen35º29'5''}{sen80º}=7.07 \ cm\end{align}$$saludos
;)
;)
Tengo una pregunta por que se usa a sobre senA y c sobre senC, eso varia o puedo usar cualquiera
;)
Hola Majo!
Los triángulos si se nombran A, B, C los ángulos en mayúscula entonces los lados se nombran en minúscula pero no a la tuntun.
A es el lado de enfrente del ángulo A
B es el lado de enfrente del ángulo B y
C es el lado de enfrente del ángulo C
De manera que en la ley de los senos, cada razón se refiere a un ángulo y su lado de enfrente o opuesto.
SAludos
;)
;)
;
a opuesto a A
b opuesto a B
c el opuesto a C
;)
¿Cómo has hecho para que la segunda vez aparecieran en minúscula las letras a b y c de comienzo de línea? - Valero Angel Serrano Mercadal
las he escrito en minúscula, y no he hecho nada especial. Ya decía yo ,que la primera vez ya las había escrito bien. !! - Lucas m
Pues es muy raro, muchas veces el corrector las pone en mayúscula y fastidia como te había fastidiado la primera vez. No entiendo nada. - Valero Angel Serrano Mercadal