¿Cómo demostrar que a ecuación representa una parábola?

---

..

¡Hola Nestor!

Hay que ver si la ecuación se puede poner de la forma

(x-h)^2 = 2p(y-k)

o

(y-k)^2 = 2p(x-h)

En otros libros en vez de 2 es 4 pero yo usaré el 2 de toda mi vida

4x^2 - 20x - 24y + 97 = 0

Bueno, ya tenemos claro que la x sea la que tenga el cuadrado y que existirá valor para h distinto de 0 porque hay un término con la x normal

Aunque nos metamos en fracciones lo mejor es dividir todo por 4 para que la x^2 quede con coeficiente 1

$$\begin{align}&x^2-5x- 6y+\frac{97}{4}=0\\&\\&\text{para obtener el }-5x, \text{el segundo término del}\\&\text {binomio de Newton }(x+k) = x^2+2k+k^2\\&\text{debe ser }k-\frac {5}{2}\\&\\&\left(x-\frac 52\right)^2=x^2-5x+\frac {25}{4}\\&\\&\text{Si ponemos este binomio al cuadrado}\\&\text{tendremos que restar }\frac {25}{4} \text{para que quede}\\&\text{lo mismo que antes}\\&\\&\left(x-\frac 52\right)^2-\frac{25}{4}- 6y+\frac{97}{4}=0\\&\\&\left(x-\frac 52\right)^2+18- 6y=0\\&\\&\left(x-\frac 52\right)^2=6y-18\\&\\&\text{tomando p=3}\\&\\&\left(x-\frac 52\right)^2= 2·3\left(y-3\right)\\&\\&\text{Luego es una parábola, se adecua a su ecuación}\\&\\&\text{El vértice es el (h,k) de la fórmula}\left(\frac 52,3\right)\\&\\&\text{El foco está a }\frac p2\text{ del vértice en este caso en}\\&\text{vertical y en sentido positivo por ser }p\gt 0\\&F=\left(\frac 52,3\right)+\left(0,\frac 32\right)=\left(\frac 52,\frac {9}{2}\right)\\&\text{La directriz es horizontal en este caso y a distancia} -\frac p2\\&\\&y=3-\frac 32 \\&\\&y=\frac 32\\&\\&\end{align}$$

Aquí tenemos  la gráfica:

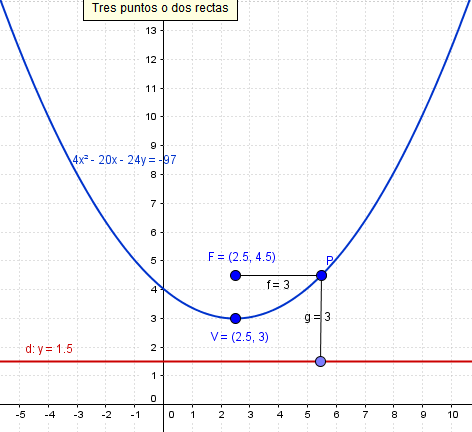
Y ya lo tienes.

Sa lu dos.

--

...