¿Alguien que pueda resolver este ejercicio?
Hallar la solución general de la siguiente ecuación como una serie de potencial alrededor del punto x=0
2𝑦 ′′ + 𝑥𝑦 ′ +𝑦 = 0
1 respuesta
·
¡Hola Mercedes!
Tomaremos como solución una serie de potencias en torno a cero y le haremos cumplir la ecuación diferencial para calcular todos los coeficientes o los que se pueda y tengamos tiempo.
$$\begin{align}&y=\sum_{n=0}^{\infty}C_nx^n\\&\\&y'=\sum_{n=1}^{\infty} C_n·nx^{n-1}\\&\\&y''=\sum_{n_2}^{\infty}C_n·n(n-1)x^{n-2}\\&\\&2\sum_{n_2}^{\infty}C_n·n(n-1)x^{n-2}+x\sum_{n=1}^{\infty} C_n·nx^{n-1}+\sum_{n=0}^{\infty}C_nx^n=0\\&\\&\text{la x esa la metemos dentro del sumatorio}\\&\\&2\sum_{n=2}^{\infty}C_n·n(n-1)x^{n-2}+\sum_{n=1}^{\infty} C_n·nx^{n}+\sum_{n=0}^{\infty}C_nx^n=0\\&\\&\text{Vemos que los exponentes arrancan en 0,1 y 0}\\&\text{Para que todos arranquen igual sacamos fuera}\\&\text{ los términos con exponente 0}\\&\\&2C_2·2·1·x^0+C_0x^0 +\\&+2\sum_{n=3}^{\infty}C_n·n(n-1)x^{n-2}+\sum_{n=1}^{\infty} C_n·nx^{n}+\sum_{n=1}^{\infty}C_nx^n=0\\&\\&\text{Simplificamos y agrupanos dos sumatorios que}\\&\text{empiezan en el mismo y tienen los mismos exponentes}\\&\\&4C_2+C_0 +2\sum_{n=3}^{\infty}C_n·n(n-1)x^{n-2}+\sum_{n=1}^{\infty} C_n·(n+1)x^{n}=0\\&\\&\text{Ahora en el primer sumatorio hacemos el cambio} \\&k=n-2\implies n=k+2\\&\\&4C_2+C_0 +2\sum_{k=1}^{\infty}C_{k+2}·(k+2)(k+1)x^{k}+\sum_{n=1}^{\infty} C_n·(n+1)x^{n}=0\\&\\&\text{Ahora podemos hacer uno solo de los dos}\\&\\&4C_2+C_0 +\sum_{k=1}^{\infty}\bigg(2·C_{k+2}·(k+2)(k+1)+C_k(k+1)\bigg)x^n=0\\&\\&\text{Y ahora poco a poco vamos calculando coeficientes}\\&\\&4C_2+C_0=0\implies \\&C_2=-\frac{C_0}{4}\\&\\&2C_3·3·2+C_1·2=0\implies12C_3+2C_1=0\implies \\&C_3=-\frac {C_1}{2·3}\\&\\&2C_4·4·3+C_2·3=0\implies24C_4+3C_2=0\implies\\&C_4=-\frac{C_2}{2·4}=\frac{C_0}{2·4·4}\\&\\&2C_5·5·4+C_3·4=0\implies40C_5+4C_3=0\implies\\&C_5=-\frac{C_3}{2·5}=\frac{C_1}{2·5·2·3}\\&\\&2C_6·6·5+C_4·5=0\implies60C_6+5C_4=0\implies\\&C_6=-\frac{C_4}{2·6}=-\frac{C_0}{2·6·2·4·4}\\&\\&2C_7·7·6+C_5·6=0\implies84C_7+6C_5=0\implies\\&C_7=-\frac{C_5}{2·7}=-\frac{C_0}{2·7·2·5·2·3}\\&\\&2C_8·8·7+C_6·7=0\implies112C_8+7C_5=0\implies\\&C_8=-\frac{C_6}{2·8}=\frac{C_0}{2·8·2·6·2·4·4}\\&\\&\text{Y tras pensarlo mucho, la regla de formación es}\\&\\&C_{2n}=\frac{(-1)^nC_0}{2^{2n}· n!}\\&\\&C_{2n+1}=\frac{(-1)^nC_1}{\frac{(2n+1)!}{n!}}\\&\\&y=C_0\sum_{n=0}^{\infty}\frac{(-1)^nx^{2n}}{2^{2n}· n!}+C_1\sum_{n=0}^{\infty}\frac{(-1)^nx^{2n+1}}{\frac{(2n+1)!}{n!}}\\&\\&\text{Los primeros términos son}\\&\\&y=C_0\left(1-\frac {x^2}{4}+\frac{x^4}{32}-\frac{x^6}{384} +\frac{x^8}{6144} \right)+\\&\quad +C_1\left(x-\frac{x^3}{6}+\frac{x^5}{60}-\frac{x^7}{840} + \frac{x^9}{15120}\right)\end{align}$$..
..
Se puede mejorar la respuesta, si nos fijamos un poco:
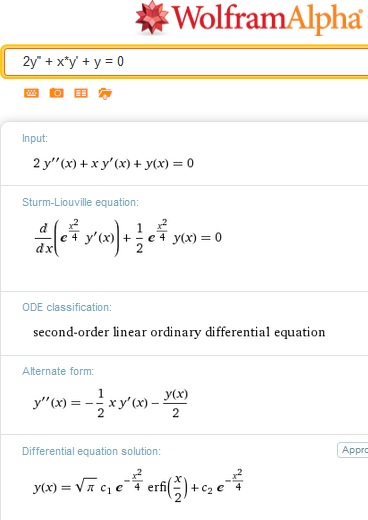
$$\begin{align}&y=C_0\sum_{n=0}^{\infty}\frac{(-1)^nx^{2n}}{2^{2n}· n!}+C_1\sum_{n=0}^{\infty}\frac{(-1)^nx^{2n+1}}{\frac{(2n+1)!}{n!}}=\\&\\&C_0\sum_{n=0}^{\infty}\frac{(-1)^n}{n!}\left( \frac{x^2}{4} \right)^n+C_1\sum_{n=0}^{\infty}\frac{(-1)^nx^{2n+1}}{\frac{(2n+1)!}{n!}}\\&\\&y=C_0\,e^{-\frac{x^2}4}+C_1\sum_{n=0}^{\infty}\frac{(-1)^nx^{2n+1}}{\frac{(2n+1)!}{n!}}\end{align}$$Eso lo sabía hacer yo. Ahora bien, WolframAlpha también reduce el segundo sumatorio a una función eso sí, una función especial.}
La llama función erfi(x), por si tú la conoces y sabes aplicar este es el resultado final donde su C2 es mi C0
·
·
Y esto dice la Wikipedia respecto de esta función final:
He intentado yo transformar el sumatorio de C1 en esa función especial pero no me sale, es un tema que no manejo y no sé si será fácil hacerlo o será muy complicado.
Y ya dejo el ejercicio, espera que te sirva lo que he hecho.
$$\begin{align}&:\end{align}$$
