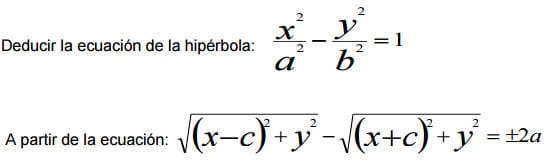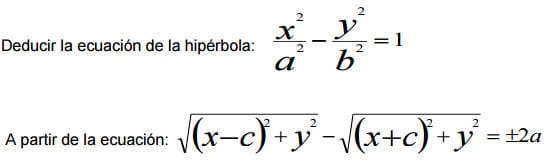Deducir la ecuación de la hipérbola

·

·

¡Hola Luk Darki!

Esto tiene que ser casi igual que la de la elipse que he hecho antes, copiaré y cambiaré algún signo.

$$\begin{align}&\sqrt{(x-c)^2+y^2}-\sqrt{(x+c)^2+y^2}=\pm2a\\&\\&\sqrt{(x-c)^2+y^2}=\pm 2a+\sqrt{(x+c)^2+y^2}\\&\\&\text{elevo al cuadrado}\\&\\&(x-c)^2+y^2=4a^2+(x+c)^2+y^2+4a^2\pm 4a \sqrt{(x+c)^2+y^2}\\&\\&x^2+c^2-2cx+y^2=x^2+c^2+2cx+y^2+4a^2 \pm 4a \sqrt{(x+c)^2+y^2}\\&\\&-2cx=2cx+4a^2\pm4a \sqrt{(x+c)^2+y^2}\\&\\&-4cx-4a^2=\pm4a \sqrt{(x+c)^2+y^2}\\&\\&cx+a^2=\pm a \sqrt{(x+c)^2+y^2}\\&\\&\text{Volvemos a elevar al cuadrado}\\&\\&c^2x^2+a^4+2a^2cx=a^2[(x+c)^2+y^2]\\&\\&c^2x^2+a^4+2a^2cx=a^2[x^2+c^2+2cx+y^2]\\&\\&c^2x^2+a^4+2a^2cx=a^2x^2+a^2c^2+2a^2cx+a^2y^2\\&\\&c^2x^2+a^4=a^2x^2+a^2c^2+a^2y^2\\&\\&\text{pasamos a la derecha}\\&\\&a^2x^2-c^2x^2+a^2y^2+a^2c^2-a^4=0\\&\\&(a^2-c^2)x^2+a^2y^2=a^4-a^2c^2\\&\\&(a^2-c^2)x^2+a^2y^2=a^2(a^2-c^2)\\&\\&\text{pasamos dividiendo lo de la derecha}\\&\\&\frac{x^2}{a^2}+\frac{y^2}{(a^2-c^2)}=1\\&\\&\text{Y en la hipérbola los semiejes y semidistancia focal cumplen}\\&\\&c^2=a^2+b^2\\&\\&a^2-c^2=-b^2\\&\\&\text{sustituyendo }\\&\\&\frac{x^2}{a^2}+\frac{y^2}{-b^2}=1\\&\\&\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\\&\end{align}$$

Y ya está.  S a l u d o s.

::

-