Formas básicas de las Tablas de Verdad y del uso de las Leyes de Inferencia
A través de las dos formas básicas de uso de las Tablas de Verdad y del uso de las Leyes de Inferencia demostrar la validez o no validez del argumento dado
- Si Bibiana aprueba el periodo académico entonces Johanna y Santiago sus hermanos se enojan con ella. Y si no aprueba el periodo académico, pierde los beneficios de la beca obtenida en la Universidad. Pero, Bibiana aprueba el periodo académico o no lo aprueba. Por lo tanto, Johanna y Santiago sus hermanos se enojan con ella o pierde los beneficios de la beca obtenida en la Universidad.
Hago alusión que lo siguiente lo ha desarrollado Valero Angel Serrano Mercadal. (Muchas gracias)
- La estructura del enunciado corresponde a un razonamiento
Las proposiciones simples son:
p: Bibiana aprueba el periodo académico
q: Johanna y Santiago sus hermanos se enojan con ella
R : pierde los beneficios de la beca obtenida en la Universidad
Y las proposiciones compuestas:
Premisa 1
- a) p q
Premisa 2
- b) ¬p r
Y la conclusión:
Conclusión
- c) Q v r
La conclusión no añade nada nuevo a lo que lo dicen las premisas. Si las premisas son verdaderas la conclusión no podrá ser falsa, cosa que sí puede suceder con los otros métodos.
Una proposición que dice:
Pero, Bibiana aprueba el periodo académico o no lo aprueba
Es redundante e innecesaria, en lógica las proposiciones solo pueden ser verdaderas o falsas como hemos visto a lo largo del curso,
p v p = 1
No aporta absolutamente nada.
Entonces:
Si se cumple p se cumple q y por tanto se cumple q v r, ya que 1+r=1
Y si no se cumple p se cumple r y por tanto se cumple q v r, ya que q+1=1
Luego siempre se cumple q v r
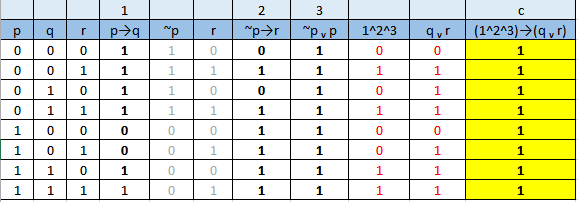
Para la tabla de la verdad la proposición que debe ser verdadera siempre es
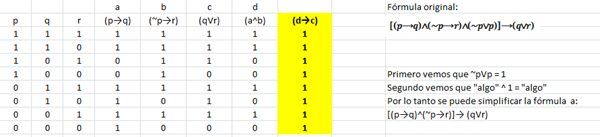
[(p q)^(¬p r)] (q v r)
- La corrección que tuve fue la siguiente:
[(𝑝⟶𝑞)∧(∼𝑝⟶𝑟)∧(∼𝑝∨𝑝)]⟶(𝑞∨𝑟)
Mis preguntas son:
- ¿Teniendo en cuenta la corrección de la formula las premisas y conclusión cambian? Si es así, ¿Cómo quedaría?
- ¿Cómo quedaría la tabla de la verdad?
2 Respuestas
No vi cual era el resultado original, pero te dejo la nueva tabla de verdad, que muestra que es una tautología, y a partir de esto vos podrás compararlo contra el resultado anterior para ver si cambió o no.
·
·
¡Hola Fredy!
Yo eliminé una premisa porque como se cumple siempre es el elemento neutro de la conjunción de proposiciones y era innecesaria, pero i el profesor quiere que la pongas la ponemos.
No cambia absolutamente nada, es más, el profesor la podría haber dado por buena sin tener que hacer ningunad corrección. Ten en cuenta que mientras no tengamos los mismos apuntes y hayamos ido a a sus clases no podemos responder exactamente de la forma que el quiera, luego si es así de rebuscado tendrás que adaptar lo que te decimos a su forma de hacer las cosas. Como te decía la proposición (~p v p) es desechable es algo que se cumple siempre y por lo tanto no aporta nada.
p: Bibiana aprueba el periodo académico
q: Johanna y Santiago sus hermanos se enojan con ella
R : pierde los beneficios de la beca obtenida en la Universidad
Y las proposiciones compuestas
1) p⟶q
2) ~p⟶r
3) ~p∨p
Y la conclusión
C) q ∨ r
De acuerdo con esto hay que hacer la tabla de verdad de
((p⟶q) ^ (~p⟶r) ^ (~p∨p)]⟶(q ∨ r)
Y eso es todo, saludos.
:
: