Anónimo
Inecuaciones con valor absoluto en ambos lados
1)
$$\begin{align}&|x+8| < |3x+5|\end{align}$$2)
$$\begin{align}&|7x+6|< |2x-1|\end{align}$$(en el anterior es menor o igual que )
3)
$$\begin{align}&|x-2|<|2x+3|\end{align}$$Por favor, sé que hay que elevar al cuadrado, pero no me da.Necesito
1 Respuesta
·
·
¡Hola Anónimo!
Somos firmes defensores de un ejercicio por pregunta explicado y bien resuelto. Si quieres los otros mándalos en otras preguntas.
Para resolver ests inecuaciones de valores absolutos tienes dos formas. La primera es calcular los puntos donde cambian de signo los valores absolutos y plantear asi cuatro inecuaciones distintas con el inconveniente de que las respuestas las tienes que intersectar con la condición de cada caso, es un lío.
Y la segunda forma es elevar al cuadrado en los dos lados.
$$\begin{align}&|x+8| < |3x+5|\\&\\&|x+8|^2 < |3x+5|^2\\&\\&x^2+16x+64 \lt 9x^2+30x+25\\&\\&0\lt 8x^2+14x -39\\&\\&\text{para entendernos mejor}\\&\\& 8x^2+14x -39>0\\&\\&\text{Es una parábola con forma de U, es}\\&\text{mayor que 0 al principio y al final, y entre}\\&\text{las raíces es menor}\\&\\&x=\frac{-14\pm \sqrt{14^2+4·8·39}}{16}=\frac{-14\pm 38}{16}\\&\\&x_1=-\frac {13}4\\&x_2=\frac 32\\&\\&\text{Luego la solución es}\\&\\&S=\left(-\infty, \frac{-13}{4}\right)\cup \left( \frac{3}{2},\infty\right)\end{align}$$Las raíces no entran por no tener el igual la inecuación.
Esta es la grafíca para comprobarlo, tomamos la función
f(x) = |x+8|-|3x+5|
la cual es negativa donde se cumple la inecuación.
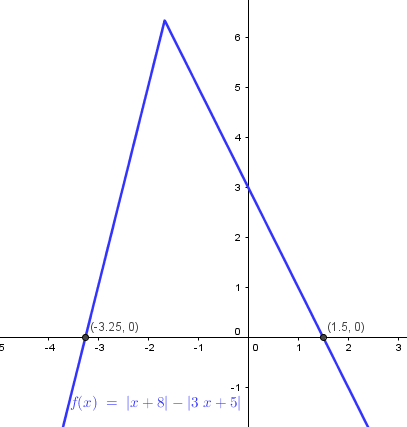
Luego las repuestas que hemos dado están bien.
Y eso es todo, sa lu dos.
:
: