Calcular la longitud de curva

;)
Hola Jaime soto!

Esa curva es:

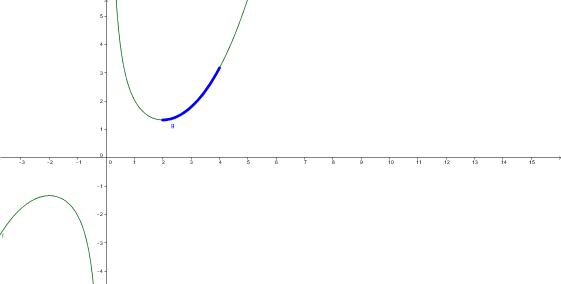
La longitud de una curva se calcula con la integral:

$$\begin{align}&\int_a^b \sqrt{1+[f'(x)]^2}dx=\\&\\&f(x)=\frac{x^4+48}{24x}\\&\\&f'(x)=\frac{4x^3(24x)-(x^4+48)24}{(24x)^2}=\frac{4x^4-x^4-48}{24x^2}=\frac{3x^4-48}{24x^2}\\&\\&1+[f'(x)]^2=1+\Bigg[\frac{3x^4-48}{24x^2}\Bigg]^2=\frac{24^2x^4+9x^8-288x^4+48^2}{24^2x^4}=\\&\\&\frac{9x^8+288x^4+48^2}{24^2x^4}=\frac{9(x^8+32x^4+256)}{24^2x^4}=\frac{9(x^4+16)^2}{24^2x^4}\\&\\&\int_2^4 \sqrt{1+f'^2}dx=\int_2^4  \sqrt{\frac{9(x^4+16)^2}{24^2x^4}} dx= \int_2^4 \frac{3(x^4+16)}{24x^2}dx=\\&\\&\frac{1}{8} \int_2^4 \frac {(x^4+16)}{x^2}dx=  \frac{1}{8} \int_2^4 (x^2+16x^{-2})dx=\\&\\&\frac{1}{8} \Bigg[ \frac{x^3}{3}-\frac{16}{x} \Bigg ]_2^4=\frac{1}{8} \Big[ \frac{4^3}{3}-4-\Big(\frac{2^3}{3}-8 \Big) \Big]=\frac{17}{6}\\&;)\end{align}$$

saludos

;)

;)