·
·
¡Hola Mª Antonia!
Derivamos e igualamos a 0 para calcular los puntos críticos.
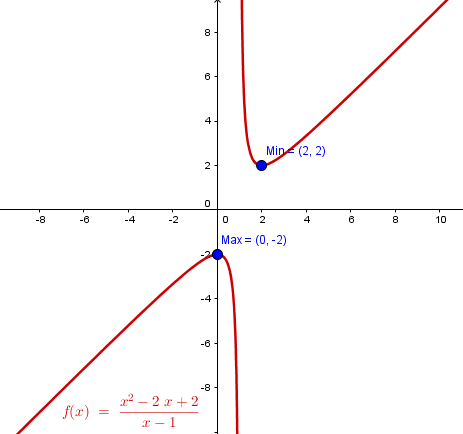
$$\begin{align}&f(x) = \frac{x^2-2x+2}{x-1}\\&\\&f'(x)=\frac{(2x-2)(x-1)-(x^2-2x+2)}{(x-1)^2}=\\&\\&\frac{2x^2-4x+2-x^2+2x-2}{(x-1)^2}=\frac{x^2-2x}{(x-1)^2}=0\\&\\&x^2-2x=0\\&\\&x(x-2)=0\\&x_1=0\\&x_2=2\\&\\&\text{tengamos en cuenta que x=1 también es un punto}\\&\text{crítico porque no existe la derivada, luego hacemos}\\&\text{estas divisiones}\\&\\&(-\infty,0)\quad f'(-1)=\frac{ 1+2}{4}\gt 0\implies creciente\\&(0,1)\qquad f'\left(\frac 12\right)=\frac{\frac 14-1}{\frac 14}=-3\lt 0\implies decreciente\\&(1,2)\qquad f'\left(\frac 32 \right)=\frac{\frac 94-3}{\frac 14}=-3\lt 0\implies decreciente\\&\\&(2,\infty)\quad f'(3)=\frac{9-6}{4}=\frac 34\gt 0 \implies creciente\end{align}$$En x=0 antes es creciente y luego decreciente, luego es un máximo relativo. Es el punto (0,-2)
En x=2 antes es decreciente y luego creciente, luego es un mínimo relativo. Es el punto (2, 2)
Fíjate como el mínimo es mayor que el máximo por eso hay que recalcar lo de relativos. Todo es culpa de lo que pasa en x=1
Y eso es todo, saludos.
:
:

