¿Cómo resolver esta ecuación logarítmica?
$$\begin{align}&2xlog_2(x)=x^2 -1\end{align}$$Tengo una ecuación que no he hallado la manera de resolver.
1 Respuesta
·
·
¡Hola Pedro!
Hay que tener mucho cuidado cuando se mezclan logaritmos con polinomios, lo normal es que salga una ecuación que no se puede resolver por métodos algebraicos. Y me parece que este es uno de esos casos.
$$\begin{align}&2xlog_2x=x^2-1\\&\\&log_2(x^{2x})= x^2-1\\&\\&x^{2x}=2^{x^2-1}\\&\\&\text{es irresoluble algebraicamente, salvo que fueran}\\&\text{soluciones comprobables trivialmente como 2,4,8..}\\&\\&(2^n)^{2·2^n}=2^{(2^n)^2-1}\\&\\&2^{2n·2^n}=2^{2^{2n}-1}\\&\\&2n2^n=2^{2n}-1\\&\\&\text{y n no puede ser entero ya que la izquierda}\\&\text{sería par y la derecha impar}\end{align}$$Pues salvo que estés dando métodos numéricos de resolución de ecuaciones, lo mejor que puedes hacer es poner la ecuación en la página WolframAlha para ver si la puede resolver.
http://www.wolframalpha.com/input/?i=2x*log_2%28x%29+%3D+x^2-1
¡Ah, pues tan preocupado de que era imposible no probé que x=1 servía de solución, pero ahí puedes ver que hay otras dos soluciones aparte que no podrías calcular de forma algebraica.
Este es el collage de dos imágenes unidas de la página, aunque puedes verla bien pinchando en el enlace de arriba.
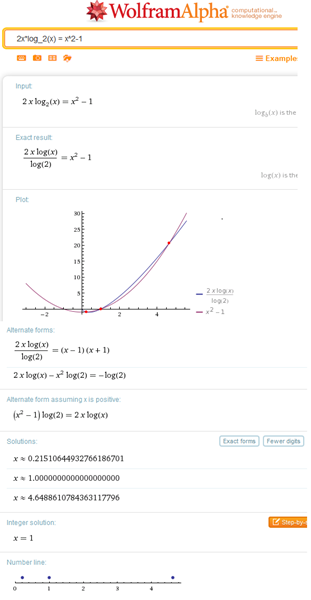
Y eso es todo saludos.
:
:
