Hallar la ecuacion de la hiperbola
La excentricidad de una hiperbola es 2 y sus focos coinciden con los focos de la elipse de ecuacion 9x^2+25y^2-90x-150y+225=0. Halla la ecuacion de la hiperbola
1 Respuesta
Respuesta de Lucas m
1
;)
Hola Gustavo!
Completamos cuadrados (compensando términos independientes):
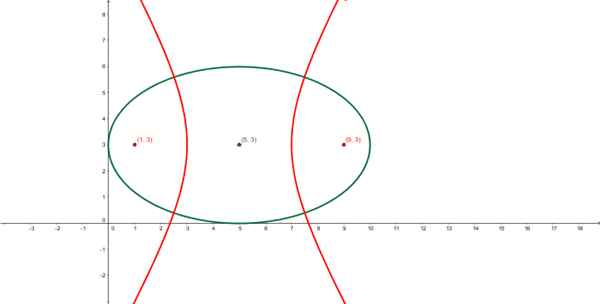
$$\begin{align}&9x^2+25y^2-90x-150y+225=0\\&\\&agrupando \ términos:\\&(9x^2-90x)+(25y^2-150y)+225=0\\&\\&9(x^2-10x)+25(y^2-6y)+225=0\\&\\&9(x-5)^2-225+25(y-3)^2-225+225=0\\&\\&9(x-5)^2+25(y-3)^2=225\\&\\&dividiendo \ por \ 225\\&\\&\frac{9(x-5)^2}{225}+\frac{25(y-3)^2}{225}=1\\&\\&\frac{(x-5)^2}{25}+\frac{(y-3)^2}{9}=1\\&\\&Centro(5,3)\\&c^2=a^2-b^2=25-9=16\\&c=4\\&F=(5+4,3)=(9,3)\\&F=(5-4,3)=(1,3)\\&\\&hipérbola:\\&e=2=\frac{c}{a}\\&\\&a=\frac{c}{2}=\frac{4}{2}=2\\&\\&c^2=a^2+b^2 \Rightarrow b^2=c^2-a^2=4^2-2^2=12\\&\\&\frac{(x-5)^2}{4}-\frac{(y-3)^2}{12}=1\end{align}$$los centros coinciden
Saludos
;)
;)
