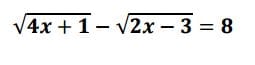Resuelva la siguiente ecuación con radicales y compruebe su solución:
- Agradezco la ayuda de alguien que Resuelva la siguiente ecuación con radicales y compruebe su solución:
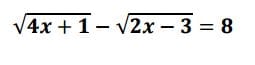
2 Respuestas
Respuesta de Valero Angel Serrano Mercadal
1
·
·
¡Hola Fabiancho!
Es mejor pasar uno radical al otro lado que tener los dos en el mismo.
$$\begin{align}&\sqrt{4x+1}= 8 + \sqrt{2x-3}\\&\\&\text{elevamos al cuadrado}\\&\\&4x+1=64 + 16 \sqrt{2x-3}+2x-3\\&\\&\text{Todo lo que no es radical al otro lado}\\&\\&4x+1-64-2x+3=16 \sqrt{2x-3}\\&\\&2x-60 = 16 \sqrt{2x-3}\\&\\&\text{elevamos otra vez al cuadrado}\\&\\&4x^2-240x+3600=256(2x-3)\\&\\&4x^2-240x + 3600 = 512x - 768\\&\\&4x^2-752x+4368 = 0\\&\\&\text{dividimos por 4}\\&\\&x^2- 188x+1092 = 0\\&\\&x= \frac{188\pm \sqrt{188^2-4·1092}}{2}=\\&\\&\frac{188\pm \sqrt{30976}}{2}=\frac{188\pm176}{2}\\&\\&x_1=182\\&x_2=6\\&\\&\text{Vamos a verificarlas}\\&\\&\sqrt{4·182+1}-\sqrt{2·182-3}=\\&\\&\sqrt{729}-\sqrt{361}= 27-19 =8\text{ vale}\\&\\&\sqrt{4·6+1}-\sqrt{2·6-3}= 5-3=2\text{ no vale}\end{align}$$Luego lo ínica respuesta es x=182
Y eso es todo, sa lu dos.
:
:
Respuesta de antoniomallo
1
Hacemos el siguiente cambio
$$\begin{align}&\sqrt{4x+1}=y\\&\end{align}$$Elevamos al cuadrado y despejamos x en función de y
$$\begin{align}&4x+1=y^2\\&\\&x=\frac{y^2-1}{4}\end{align}$$Sustituimos el valor de x en la ecuación dada
$$\begin{align}&y-\sqrt{2·\frac{(y^2-1)}{4}-3}=8\end{align}$$Operamos y despejamos la y
$$\begin{align}&\sqrt{\frac{2y^2-2}{4}-3}=y-8\\&\\&\frac{2y^2-2}{4}-3=y^2-16y+64\\&\\&2y^2-2-12=4y^2-64y+256\\&\\&2y^2-64y+270=0\\&\\&y=\frac{64\pm \sqrt{4096-2160}}4\\&\\&y_1=27\\&y_2=5\\&\\&\end{align}$$Para cada valor de y encontramos un valor de x:
$$\begin{align}&\sqrt{4x+1}=y\\&\\&4x+1=y^2\\&\\&x=\frac{y^2-1}{4}\\&\\&\text{Para cada valor de y encontramos un valor de x:}\\&\\&x_1=182\\&x_2=6\\&\end{align}$$
Como el valor de x2 = 6 no cumple la igualdad, la solución es x = 182