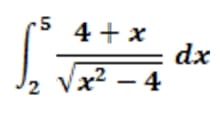Resorber las siguientes ejercicios de calculo

·

·

¡Hola Esneider!

No es sencilla, te ayudaré pero no lo haré todo.

Dividiremos la integral en dos.

$$\begin{align}&\int \frac{4+x}{\sqrt{x^2-4}}dx=\\&\\&\int \frac{4}{\sqrt{x^2-4}}dx+\int \frac{x}{\sqrt{x^2-4}}dx=\\&\\&\text{La segunda es inmediata en la práctica}\\&\\&\int \frac{4}{\sqrt{x^2-4}}dx+\sqrt{x^2-4}=\end{align}$$

Y para la primera te voy a dar este enlace donde se resuelve una similar

http://www.todoexpertos.com/preguntas/733bokh7v9f4o96h/el-tema-es-de-analisis-matematicas-calculo?selectedanswerid=734wof99f3vrrfn8&nid=hsjprselgwjq9uct97r6ngsm9kupxsksa8m69wmlhcm9vh4t97&utm_source=todoexpertos&utm_medium=EmailNotification&utm_campaign=FollowedQuestion_AnswerSolvedAdded 

Te digo cuál es el resultado que debe darte

$$\begin{align}&I=4\,ln\left(x+\sqrt{x^2-4}\right)+\sqrt{x^2-4}\\&\\&\text{Luego la integral definida es}\\&\\&I_2^5=4\,ln\left(5+\sqrt{5^2-4}\right)+\sqrt{5^2-4}-4\,ln\left(2+\sqrt{2^2-4}\right)-\sqrt{2^2-4}=\\&\\&4\,ln(5+\sqrt{21})+\sqrt {21}-4\,ln\,2\end{align}$$

Y eso es todo, sa lu dos.

:

: