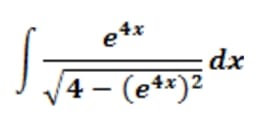Resolver los siguientes cálculos integral
El texto de la pregunta debe ser al menos de 60 caracteres. El texto de la pregunta debe ser al menos de 60 caracteres.
1 Respuesta
Respuesta de Valero Angel Serrano Mercadal
1
·
·
¡Hola Andrés!
Vamos a hacer modificaciones de forma, pero no de valor, que hagan que tengamos dentro de la integral la derivada exacta de un arco seno.
$$\begin{align}&\int \frac{e^{4x}}{\sqrt{4-(e^{4x})^2}}dx=\\&\\&\int \frac{e^{4x}}{\sqrt{4\left(1-\frac{(e^{4x})^2}4\right)}}dx=\\&\\&\frac 12\int \frac{e^{4x}}{ \sqrt{1-\left(\frac{e^{4x}}2\right)^2}}dx=\\&\\&\text{tengamos en cuenta que }\left(\frac{e^{4x}}2\right)'=2e^{4x}\\&\text{necesitamos que el numerador tenga eso}\\&\\&=\frac 12·\frac 12\int \frac{2e^{4x}}{ \sqrt{1-\left(\frac{e^{4x}}2\right)^2}}dx=\\&\\&\text{ya tenemos dentro una derivada exacta}\\&\\&=\frac 14 arcsen\left(\frac{e^{4x}}2\right)+C\\&\\&\end{align}$$Y eso es todo, sa lu dos.
:
:
