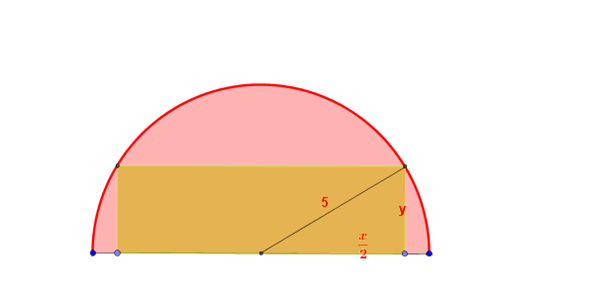
¿Cuál es el perímetro máximo que puede tener un rectángulo inscrito en un semicírculo de radio 5 unidades?
Realice el esquema y al lado del rectángulo le di un variable X e Y en el cual dentro de esta se formara un triangulo rectángulo ya que su hipotenusa seria 5 por el radio, luego utilice pitágoras para relacionar las variables y luego despejar y para después reemplazar en la ecuación de su perímetro (P(x)= 2x+2y)
2 Respuestas
;)
Hola Anyara!
P=2x+2y
$$\begin{align}&5^2=(\frac{x}{2})^2+y^2\\&\\&25=\frac{x^2}{4}+y^2\\&\\&y^2=25- \frac{x^2}{4}=\frac{100-x^2}{4}\\&\\&y=\frac{\sqrt{100-x^2}}{2}\\&\\&P(x)=2x+2 \frac{\sqrt{100-x^2}}{2}=2x+ \sqrt{100-x^2}\\&\\&Derivando:\\&P'(x)=2 + \frac{1}{2 \sqrt {100-x^2}}(-2x)=2 - \frac{x}{ \sqrt {100-x^2}}\\&\\&P'(x)=0\\&\\&2=\frac{x}{ \sqrt {100-x^2}}\\&\\&2 \sqrt{100-x^2}=x\\&\\&4(100-x^2)=x^2\\&\\&400=5x^2\\&\\&x^2=80\\&\\&x=\sqrt{80}=4 \sqrt 5 \simeq 8.9\\&\\&y=\frac{\sqrt{100-80}}{2}=\frac{\sqrt{20}}{2}=\sqrt 5\\&\\&Comprovación \ Máximo\\&P'(8)=2- \frac{8}{\sqrt{100-64}}=\frac{2}{3}>0 \Rightarrow Creciente\\&\\&P'(9)=2- \frac{9}{\sqrt{100-81}}=-0.064 <0 \ Decreciente\\&\\&\Longrightarrow MAXIMO\\&(4 \sqrt 5, \sqrt 5)\\&\end{align}$$Saludos
;)
;)
Estos problemas lo resolves formando la relación incógnita que te piden ... perímetro ... en función del único dato... que seria el radio = 5 unidades. Luego aplicas la condición de derivada primera = 0 y hallarías lo que te piden.
Hace el dibujo del rectángulo. Si la base del rectángulo ( eje x) la llamas 2a y la altura b ( eje y) ... podes establecer:
Perimetro.........= 10 - a + 10 - 2 b = 20 - a - 2b ( 1)
Por otro lado = (a/2)^2 + b^2 = 25 (2)
De (2) ..........................b =( 25 - (a/2)^2)^1/2 ....................si lo llevas a la (1) tendrias:
Perímetro( a) = 20 - a - 2 ( 25 - (a/2)^2)^1/2 ... que la derivas una vez y te da:
d(Perímetro) / da =( a / (100 - a^2)^1/2) - 1 ...igualándola a 0 ... te da:
a= 5V2
B lo hallarías directamente de la relación (1).
Corrijo... segundo párrafo dice:
Hace el dibujo del rectángulo. Si la base del rectángulo ( eje x) la llamas 2a y la altura b ( eje y) ... podes establecer:
Debes tomar base = a .( y no 2a) ... resto del desarrollo como te lo escribí.