Para la funcion dada determine el rango f(x)=(x+9)/√(x-8)
Para la función dada determine el rango con la explicación
2 respuestas
·
·
¡Hola Manuela!
El rango de una función es el dominio de la función inversa, luego calulemos la función inversa. Bueno, no la calcularemos del todo, pero casi.
$$\begin{align}&y = \frac{x+9}{\sqrt{x-8}}\\&\\&\text{tenemos que despejar x}\\&\\&y \sqrt{x-8}= x+9\\&\\&\text{elevamos al cuadrado}\\&\\&y^2(x-8) = x^2+18x+81\\&\\&x^2+(18-y^2)x+81+8y^2=0\\&\\&x= \frac{y^2-8\pm \sqrt{(18-y^2)^2-4(81+8y^2)}}{2}\\&\\&\text{Estará definida cuando el determinante sea no negativo}\\&\\&324-36y^2+y^4-324-32y^2\ge0\\&\\&y^4-68y^2\ge0\\&\\&y^2-68 \ge0\\&\\&y^2\ge 68\\&\\&|y| \ge \sqrt {68}\\&\\&\text{Pero siempre que se eleva al cuadrado para solucionar}\\&\text{una ecuación pueden aparecer respuestas fantasma}\\&\\&\text {Si y es negativa}\\&\\&y = \frac{x+9}{\sqrt{x-8}}\le 0\implies x+9\le 0\implies x\le-9\\&\\&\text{pero entonces}\\&\\&x-8\le-9-8=-17\\&\\&\text{con lo que no está definida }\sqrt{x-8}\\&\\&\text{luego }y \ge \sqrt {68}\\&\\&Rango f=Dom f^{-1}= [\sqrt {68},\infty)\end{align}$$Y eso es todo, sa lu dos.
:
:
;)
Hola manuela!
Recuerda votar la respuesta!
El rango de una función son los valores que toma la variable dependiente (y) para los valores de x que son posibles (Dominio de f(x); x>8)
Se obtiene calculando el Dominio de la función inversa.
Para obtener la función inversa, intercambiamos las variables (x por y, e y por x), :
Y despejamos la nueva y:
$$\begin{align}&y=\frac{x+9}{\sqrt{x-8}}\\&\\&x=\frac{y+9}{\sqrt{y-8}}\\&\\&x \sqrt{y-8}=y+9\\&\\&elevando \ al \ cuadrado:\\&x^2(y-8)=(y+9)^2\\&\\&x^2y-8x^2=y^2+18y+81\\&\\&y^2+(18-x^2)y+(81+8x^2)=0\\&\end{align}$$Como la función inicial no es inyectiva en realidad hay dos inversas , una para la rama decreciente y otra para la creciente.Saldrían de despejar la y en esa ecuación de 2ºgrado en y.
Como lo que me interesa es el rango, solo tengo que estudiar cuando esa expresión se puede calcular. Una ecuación de 2º grado tiene solución cuando su discriminante es mayor o igual que cero.
$$\begin{align}&y^2+(18-x^2)y+(81+8x^2)=0\\&\\&\Delta=discriminante=b^2-4ac \geq0\\&\\&(18-x^2)^2-4(81+x^2) \geq 0\\&\\&324-36x^2+x^4-324-32x^2 \geq0\\&\\&x^4-68x^2 \geq 0\\&\\&x^2(x^2-68) \geq0\\&\\&ordenamos \ \ de \ \ mayor \ \ a \ \ menor \ las \ raices \ del\ polinomio:\\&x=0\\&x=\pm \sqrt {68}\\&\\&\end{align}$$Y en nuestro caso el intervalo que nos interesa es
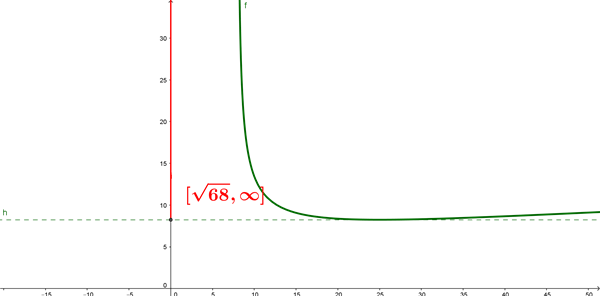
$$\begin{align}&[+\sqrt{68},+ \infty]=Rang\end{align}$$Te adjunto la gráfica.
En verde la función, en Rojo el Rango
Saludos
Recuerda votar
;)
;)
;)
Habría cuatro intervalos de signo de la función inversa
(-Infinito,-sqrt(68))
(-Sqrt(68), 0)
(0,+sqrt(68))
(+sqrt(68), + infinito)
Como el dominio de la función original es x>8, para esos valores la y>0.
La y es la x de la inversa, luego para empezar los dos primeros intervalos ((-infinito,-sqrt(68))
(-Sqrt(68), 0)
Luego solo quedan estudiar los dos últimos
(0,+sqrt(68)) da valores negativos el descriminante x^2(x^2-68)
(+sqrt(68),+infinito) da valores positivos el descriminante. Es nuestra solución
;)
;)